Having noticed a LOT of questions of solids of revolutions, I've decided to pull a
Zealous and write a little tutorial.
So what is a solid of revolution?Let's say we have this graph
)
(pictured left), and we're going to pretend that even though the graph is clearly in a two-dimensional space (only has two axis), that it's actually something third dimensional. Next, we're going to take this graph, and in our new third dimension, we're going to rotate it around the x-axis. All of a sudden, we have this new three-dimensional shape (pictured right). What can we do with this shape? Well, we can find its volume. Why are we going to find its volume? BECAUSE WE CAN!
 Oh, that's cool. How do I find the volume?
Oh, that's cool. How do I find the volume?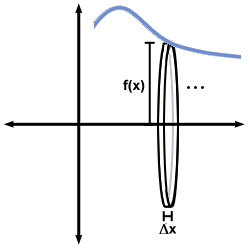 From http://img.sparknotes.com/figures/6/63c1992d178b65dd1202406ca81625b5/intapps2.gif
From http://img.sparknotes.com/figures/6/63c1992d178b65dd1202406ca81625b5/intapps2.gifWith calculus magic!

Remember in methods how you drew a bunch of rectangles to find the approximate area under a curve? Well, we're going to do that here - but instead, we're going to draw cylinders, once again pretending that we actually have three dimensions, not two.
The volume of this cylinder is given by

, and we can see that the radius is given by
)
, and the height is

. If you have trouble figuring out why, look above - notice how our cylinder is orientated?
Now, let's say we want to find the volume from

to

. Well, we're going to have to take the sum of all of those cylinders. So, if we put all of this stuff into the first formula, we get

.
Now, we wave the calculus magic wand to make everything super small (i.e. making all of those cylinders as small as possible) and we get

In fact, we can do something similar if we turn the cylinder around. In fact, if you do this, you'll find out that if we rotate it around the y-axis, we get
 Woah woah woah, slow down - how does this find the volume?
Woah woah woah, slow down - how does this find the volume?Well, think about it. If we're calculating all those really small cylinders that we've shoved under a curve, it's almost as in we're rotating the curve around the cylinder and finding everything in-between.
Yeah - I still don't understand why this works.Don't worry, that's fine - you're only in year 12, you don't need to understand calculus magic yet. You just need to know that it works!
Okay, cool. So how do we actually find these volumes?Well, remember that formula we made up there with calculus magic? We essentially just use that, but it can be difficult to just jump in with that at first. So, let's take a step-by-step process.
1. Draw your curve, and then shade in the area you want to find.Remember - finding the volume is just an extension of finding the area, so by finding the area, we're making life a lot easier for ourselves.
2. Figure out what kind of a shape you'll get.This is critical, and can even save time. Let's say you have a circle at the origin. If you rotate this around the y-axis, using your imagination you'll hopefully see a sphere. This means you can just use the formula for the volume of a sphere to confirm you get the right answer in the end.
You'll also need to do this for weird revolutions, one of which I'll show you later. For some weird revolutions, you can't just plug and play with our formula.
3. Figure out what your limits a and b are.Now that you've shaded in this area, you should know what your limits are.
4. Figure out what axis you want to rotate around.This is the crucial step - it'll determine what formula you'll use.
So, if you remember, when we rotated around the x-axis, we get a dx on the end. So, our formula for going around the x-axis is

.
Similarly, when we went around the y-axis, we got a dy on the end. So, our formula for going around the y-axis is
 5. Have I got everything?
5. Have I got everything?Limits - check. Formula - check. Knowing what our shape is - check. So let's go for it!
Note: most commonly, you'll see the formula in the form

. This is because pi is a constant, and with any constant, can be taken outside of the integral for ease of calculation.
So, is there actually a reason for doing this?Well, using this we can actually find the general formula for the volume of a solid. In fact, for fun, let's do the above to prove what the volume of a special type of ellipsoid.
 From http://upload.wikimedia.org/wikipedia/commons/thumb/5/50/Ellipsoid_tri-axial_abc.svg/200px-Ellipsoid_tri-axial_abc.svg.png
From http://upload.wikimedia.org/wikipedia/commons/thumb/5/50/Ellipsoid_tri-axial_abc.svg/200px-Ellipsoid_tri-axial_abc.svg.pngSo, we're going to consider TWO special cases. Normally, the volume of this shape is given by

, but we only have two dimensions. So let's consider the special cases where b = c (when we rotate around the x-axis) and where a = c (when we rotate around the y=axis). This gives us the two formula

and
 1. Draw your curve, and then shade in the area you want to find.
1. Draw your curve, and then shade in the area you want to find.Okay, so let's work with the x-axis first. We have a normal ellipse,

, and we want to find the area under the curve.
2. Figure out what kind of a shape you'll get.Well, looking up, we can see that I gave you the shape... Which is a little cheating, but let's ease into this step, because it is the hardest. See if you can visualize our ellipse rotating around to form the ellipsoid. In fact, bonus: can you see why b = c if we go around the x-axis and why a = c if we go around the y-axis?
3. Figure out what your limits a and b are.Looking at our shaded area, we want to go from -a to +a - limits, found!
4. Figure out what axis you want to rotate around.Okay, so first we're going to around the x-axis. So, we have a dx, and this means our formula is
 5. Have I got everything?
5. Have I got everything?Looking at the formula above, I'd say so. But, we need y^2 by itself. Some quick solving should help us find

Now, to do all the work:
-(-ab^2 + \frac{ab^2}{3})]<br />\\ V=\pi[2ab^2 -\frac{ab^2}{3}]<br />\\ V=\pi \frac{4ab^2}{3}<br />\\ \therefore V=\frac{4}{3}\pi ab^2)
Which is just what we predicted! Yay, we found the volume of this special ellipsoid! Now, for practice, I'll let you try for when we go around the y-axis. Worked solution below:
Spoiler
1. Draw your curve, and then shade in the area you want to find.Similar to before, but now you're shading the right half of the ellipse.
2. Figure out what kind of a shape you'll get.Just gotta look up again. I believe in you!

Remember, this will be the hardest step - suddenly having to visualise in the third dimension is not easy when you've spent all this time in the second.
3. Figure out what your limits a and b are.Limits are -b to +b. If you had trouble with this, go backwards and learn how to find the area between a curve and the y-axis.
4. Figure out what axis you want to rotate around.Going around y, giving us a dy. So, our formula is
 5. Have I got everything?
5. Have I got everything?Close - but once again, we need to isolate either x or y. As you can see just above this, we want x^2, so we get

Now, we plug and play:
-(-a^2b + \frac{a^2b}{3})]<br />\\ V=\pi[2a^2b -\frac{a^2b}{3}]<br />\\ V=\pi \frac{4a^2b}{3}<br />\\ \therefore V=\frac{4}{3}\pi a^2b)
Which is, once again, what we predicted!
Also, for fun - if we assume these two volumes are equal, we imply that

, and we get the volume for a sphere. How cool is that?
Yeah... Pretty much. If you want some more things to work with, message below, because as I type this, it's lunch time and I'm hungry. Come back later, and I'll have one of those tricky shapes I mentioned earlier in this how-to. Any questions on anything written here, also comment below, and myself or some other helpful user will certainly come to your aid!

