Awkward question? here's an awkward algebraic proof.
(using the CAS...)
1. Start by setting up an equation for f(x) for a cubic in intercept form. For this cubic, we have intercepts (a,0), (b,0) and (c,0):
 & = & (x-a)(x-b)(x-c)\\f'(x) & = & 3x^{2}+(-2a-2(b+c))x+a(b+c)+bc\\\end{eqnarray*}\\)
2. Use
)
to find the equation of the tangent line of this cubic function at x=p. Then let y=0 so we can solve for x, which will be the x intercept of the linear line.
\\y-f(p) & = & f'(p)(x-p)\\\\Let\ y=0\ find\ x\ intercept:\\0-f(p) & = & f'(p)(x-p)\\-\frac{f(p)}{f'(p)} & = & (x-p)\\x_{int} & = & p-\frac{f(p)}{f'(p)}\\\end{eqnarray*}\\)
3. We have now found the x intercept of the tangent to f(x) at any point x=p. Now sub in the x coordinate of the point half way between intercepts (sub this into p):
\\x_{int} & = & a\\\\Sub\ in\ p & = & \frac{a+c}{2}\\x_{int} & = & b\\\\Sub\ in\ p & = & \frac{a+b}{2}\\x_{int} & = & c\\\end{eqnarray*}\\)
So when we take the tangent line of f(x) where x is half way between the a and b, the x intercept of the tangent line will be at c. The same occurs for taking the midpoint of other intercepts.
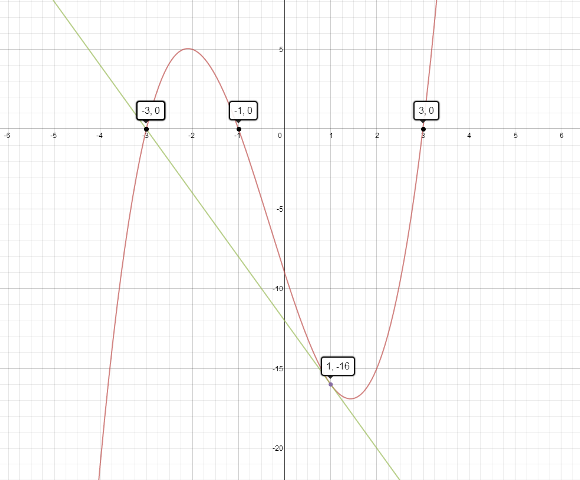
Here's a graph for those who are interested. If we take the tangent line at x=1, which is half way between the (-1,0) and (3,0) intercepts, the tangent's x intercept will be at (-3,0) which is the other intercept of the cubic graph.
=(x+1)(x-3)(x+3))
Pretty interesting question, thanks for sharing!
Home
Help
Search
Login
