EDIT: Bit late but oh well.
Just going to add to what nliu1995 has said above, as if may help to look at it visually. The cubic functions below have 0,1 and 2 stationary points.
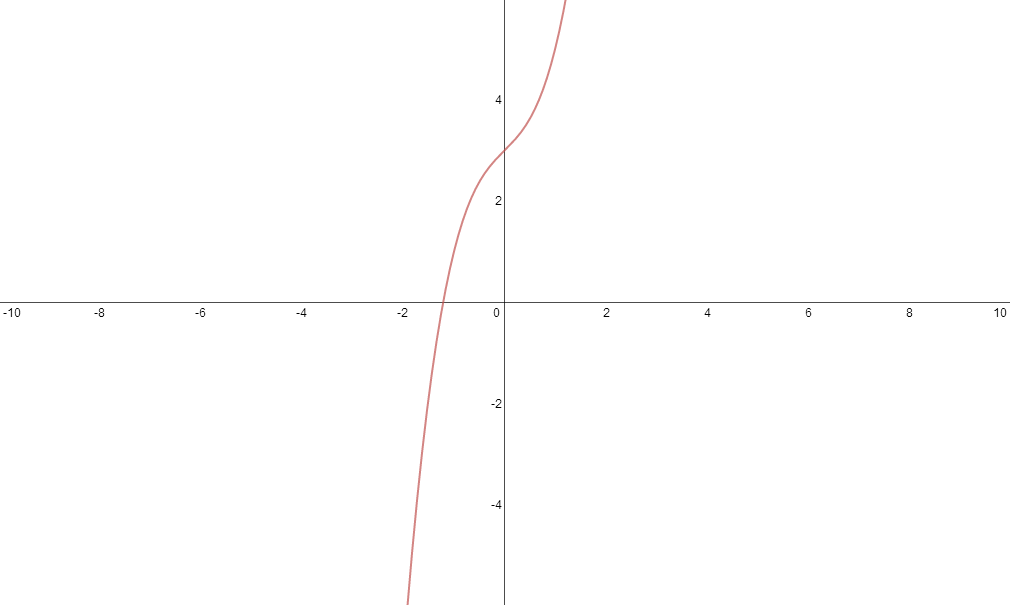
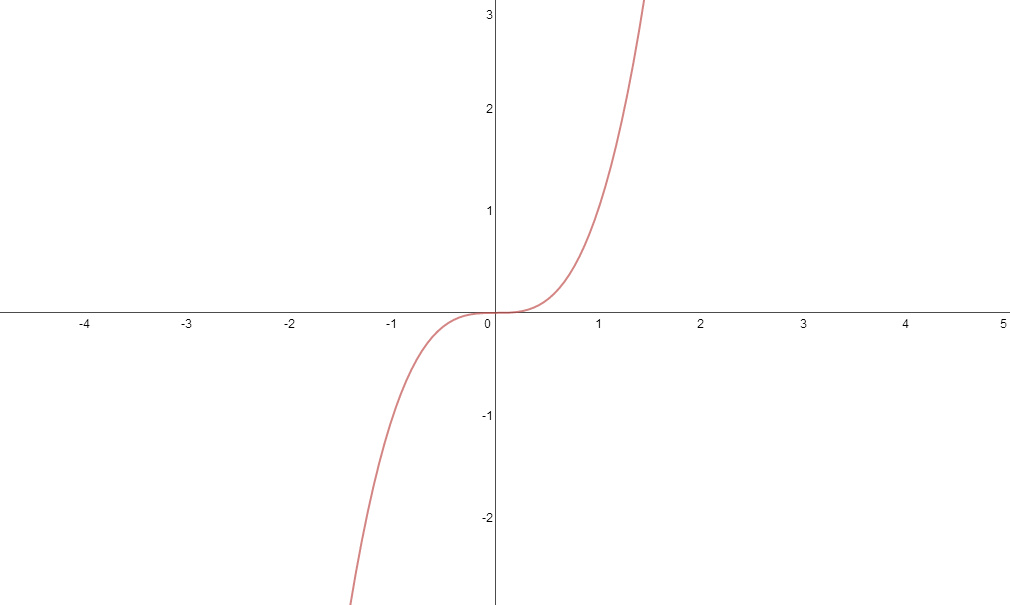
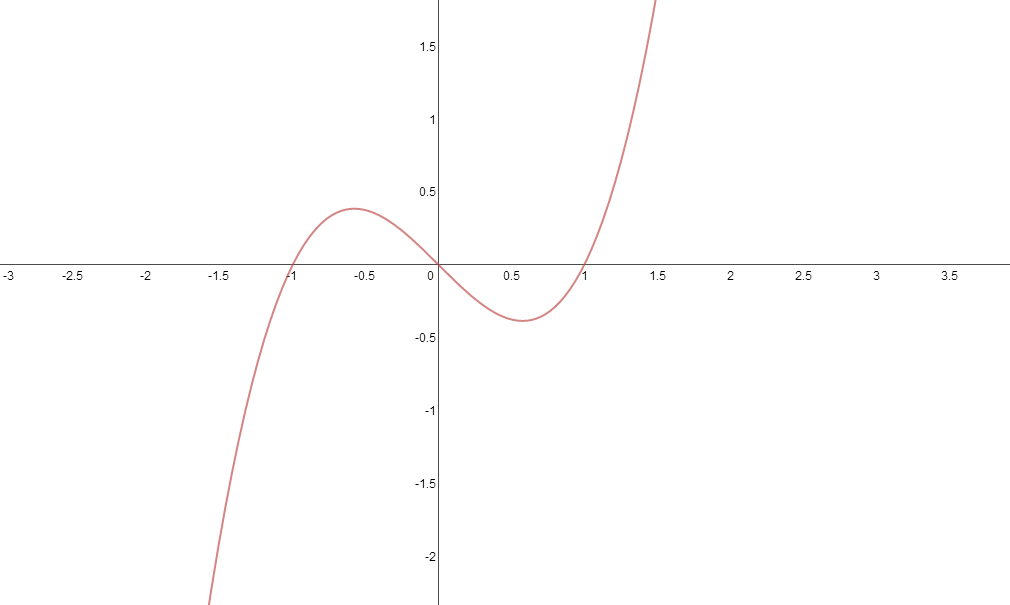
So as nliu1995 has said, if you differentiate the first, the quadratic you get will have 0 solutions, i.e. the discriminant will be less than 0.
If you differentiate the second, you will get a quadratic with a repeated root, that is only 1 unique solution, discriminant=0.
For the third, again differentiating will give a quadratic with two solutions, discriminant>0.
You don't need the above for the actual question, it's just more a way to look at it and think about it. The second point to note is that a cubic function with no stationary points (as in the first example) is not a linear function, it still has a non zero coefficient on

, it's just the
=0)
has no solutions, and so no turning points.
Anyways, hope that helps.

