Version 1.5Ok guys and girls, this is a guide/reference for using the Ti-nspire for Mathematical Methods CAS. It will cover the simplest of things to a few tricks. This guide has been written for
OS Version 3.1.0.392. To update go to
http://education.ti.com/calculators/downloads/US/Software/Detail?id=6767.
Any additions or better methods are welcomed. Also let me know if you spot any mistakes.
Guide to Using the Ti-nspire for SPECIALIST - The more intricate & complex but enjoyable: http://www.atarnotes.com/forum/index.php?topic=125433.msg466856#msg466856
Printer Friendly PDF version 1.5: http://www.atarnotes.com/?p=notes&a=feedback&id=659NOTE: There is a mistake in the printable version. Under normal distribution for pdf functions it should read "For the height of the probability curve at a certain point use [Menu] [5] [5] [1] (Pdf)"
Also under the shortcut keys the highlighting should read "Copy: Ctrl left or right to highlight, [SHIFT (the one with CAPS on it)] + [c]"Simple things will have green headings, complicated things and tricks will be in red.
Firstly some simple things. Also Note that for some questions, to obtain full marks you will need to know how to do this by hand. DON’T entirely rely on the calculator.
Solve, Factor & ExpandThese are the basic functions you will need to know.
Open Calculate (A)
Solve: [Menu] [3] [1] – (equation, variable)|Domain
Factor: [Menu] [3] [2] – (terms)
Expand: [Menu] [3] [3] – (terms)
 Matrices
MatricesMatrices can be used as an easy way to solve the ‘find the values of m for which there is zero or infinitely many solutions’ questions. When the equations

and

are expressed as a matrix

, letting the determinate equal to 0 will allow you to solve for m.
E.g. Find the values of m for which there is no solutions or infinitely many solutions for the equations 2x+3y=4 and mx+y=1
Determinant: [Menu][ 7] [3] Enter in matrix representing the coefficients, solve for det()=0

Remember to plug back in to differentiate between the solutions for no solutions and infinitely many solutions.
Modulus FunctionsWhile being written as || on paper, the function for the modulus function is abs() (or absolute function). i.e. just add in abs(function)
For example y=|x| and y=|x^2-4|

 Defining Domains
Defining DomainsWhile graphing or solving, domains can be defined by the addition of |lowerbound<x<upperbound
The less than or equal to and greater than or equal to signs can be obtained by pressing ctrl + < or >
e.g. Graph

for

Enter
=x^2 |-2<x\leq 1)
into the graphs bar
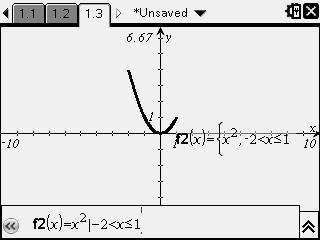
This is particulary useful for fog and gof functions, when a domain is restriced, the resulting function’s domain will also be restricted.
E.g. Find the equation of
)
when
=x^2,x \in(-2,1] )
and
=2x+1,x\in R )
1. Define the two equations in the Calulate page. [Menu] [1] [1]

2. Open a graph page and type, f(g(x)) into the graph bar

The trace feature can be used to find out the range and domain. Trace: [Menu] [5] [1]
Here
=(2x+1)^{2})
where the Domain = (-1.5,1] and Range =[0,4)
Completing the SquareThe easy way to find the turning point quickly. The Ti-nspire has a built in function for completing the square.
[Menu] [3] [5] - (function,variable)
e.g. Find the turning point of


So from that the turning point will be at (-2,1)
Easy Maximum and MinimumsIn the newer version of the Ti-nspire OS, there are functions to find maximum, minimums, tangent lines and normal lines with a couple of clicks, good for multiple choice, otherwise working would need to be shown. You can do some of these visually on the graphing screen or algebraically in the calculate window.
Maximums: [Menu] [4] [7] – (terms, variable)|domain
Minimums: [Menu] [4] [8] – (terms, variable)|domain
E.g. Find the values of x for which

has a maxmimum and a minimum for


Tangents at a point: [Menu] [4] [9] – (terms, variable, point)
Normals at a point: [Menu] [4] [A] - (terms, variable, point)
E.g. Find the equation of the tangent and the normal to the curve
^{2})
when

.
 Finding Vertical Asymptotes
Finding Vertical AsymptotesVertical Asymptotes occur when the function is undefined at a given value of x, i.e. when anything is divided by 0. We can manipulate this fact to find vertical asymptotes by letting the function equal

and solving for x.
e.g. Find the vertical asymptotes for
 ,x \in [0,\pi])
and
-2)

So for
, x \in [0,\pi])
there is a vertical asymptote at

and for
-2)
at

Don’t forget to find those other non-vertical asymptotes too.
The x-y Function TestEvery now and then you will come across this kind of question in a multiple choice section.
If
+f(y)=f(xy))
, which of the following is true?
A.
=x^2)
B.
=\ln(x) )
C.
= \frac{1}{x} )
D.
=x)
E.
=(x+2)^2)
You could do it by hand or do it by calculator. The easiest way is to define the functions and solve the condition for x, then test whether the option is true. If true is given, it is true otherwise it is false.

So option B is correct.
The Time Saver for DerivativesBy defining, f(x) and then defining df(x)= the derivative, you won’t have to continually type in the derivative keys and function. It also allows you to plug in values easily into f’(x) and f’’(x).
Derivative: [Menu] [4] [1]
E.g. Find the derivative of

Define f(x), then define df(x)

The same thing can be done for the double derivative.

Just remember to redefine the equations or use a different letter, e.g. g(x) and dg(x)
Solving For Coefficients Using Definitions of Functions Instead of typing out big long strings of equations and forgetting which one is the antiderivative and which one is the original, defined equations can be used to easily and quickly solve for the coefficients.
E.g. An equation of the form

cuts the x-axis at (-2,0) and (2,0). It cuts the y-axis at (0,1) and has a local maximum when

. Find the values of a, b, c & d.
1. Define
=ax^3+bx^2+cx+d)
(Make sure you put a multiplication sign between the letters)
2. Define the derivative of the f(x) i.e. df(x)
3. Use solve function and substitute values in, solve for a, b, c & d.


So

and

and the equation of the curve is
=\frac{1}{2}x^3-\frac{1}{4}x^2-2x+1) Deriving Using the Right Mode
Deriving Using the Right Mode The derivative of circular functions are different for radians and degrees. Remember to convert degrees to radians and be in radian mode, as the usual derivatives that you learn e.g.
)=\cos(x))
are in radians NOT degrees.
RADIAN MODE DEGREES MODE

 Getting Exact Values On the Graph Screen
Getting Exact Values On the Graph ScreenNow for what you have all been dreaming of. Exact values on the graphing screen. Now the way to do this is a little bit annoying.
1. Open up a graph window
2. Plot a function e.g.
=\sqrt[3]{x})
3. Trace the graph using [Menu] [5] [1]
4. Trace right till you hit around 0.9 or 1.2 and click the middle button to plot the point.
5. Press ESC
6. Move the mouse over the x-value and click so that it highlights, then move it slightly to the right and click again. Clear the value and enter in


.
Using tCollect to simplify awkward expressions Sometimes the calculator won’t simplify something the way we want it to. tCollect simplifies expressions that involves trigonometric powers higher than 1 or lower than -1 to linear trigonometric expressions.
 Streamlined Markov Chains
Streamlined Markov Chains For questions that require the use of the T transition matrix more than once, the following methods can be used to save time so that the T matrix does not need to be repeatedly inputted or copied down.
1. Define the T matrix as t.
2. Define the initial state matrix as s.
3. Evaluate by substituting t and s in with the appropriate powers.
E.g. For the Transition matrix

and initial state

, find S
2 and S
3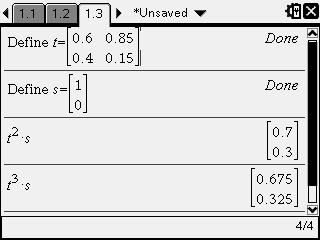 Binomial Distributions
Binomial DistributionsFor a single value of x e.g. Pr(X=2) = [Menu] [5] [5] [D] (Pdf)
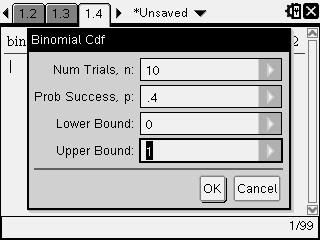
For multiple values of x e.g. Pr(X<2) = [Menu] [5] [5] [E] (Cdf)
e.g. Probability of Success = 0.4, Number of trials =10, i.e. X~Bi(10,0.4)
Find the probability of two successes and less than two successes
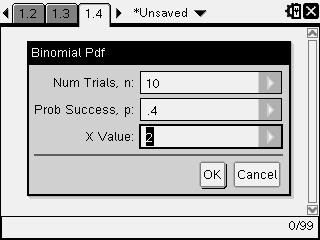

Pr(X=2)=0.1209
Pr(X<2)=0.0464
Normal DistributionsThe probability will correspond to the area under the Normal distribution curve.
For the height of the probability curve at a certain point use [Menu] [5] [5] [1] (Pdf)
From lower value to higher value = [Menu] [5] [5] [2] (Cdf) (for -∞ use ctrl +
i)
e.g. The probability of X is given by the Normal Distribution with

i.e. X~N(0,1)
Find Pr(X<1) and Pr(0<X<1)
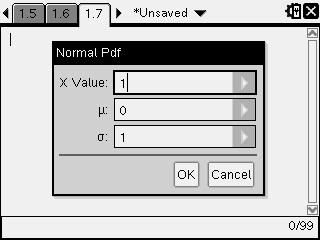
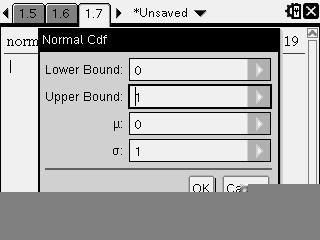
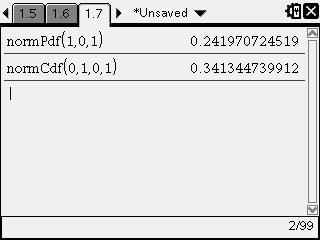
Pr(X<1)=0.2420, Pr(0<X<1)=0.3413
IntegralsUsing the integral function and solve function for probability distributions. The area under a probability distribution function must equal 1, so if we are given a function multiplied by a k constant, we can antidifferentiate the function and solve for k.
Integral: [Menu] [4] [3]
E.g. If f(x) is given by
=\begin{cases}<br />kx^{2}+1 & \text{ if } 0<x<10 \\ <br />0 & \text{ } otherwise <br />\end{cases})
, find the value of k if f(x) is to be a probability density function.
 Shortcut Keys
Shortcut KeysCopy: Ctrl left or right to highlight, [SHIFT (the one with CAPS on it)] + [c]
Paste: [Ctrl] + [v]
Insert Derivative: [CAPS] + ["-"]
Insert Integral: [CAPS] + ["+"]
∞: [Ctrl] + ["
i"]
Thanks to Jane1234 & duquesne9995 for the shortcut keys. Thanks to Camo and SamiJ for finding the errors.

