How do you find the volume of revolution about the y axis of the area under the graph y=sqrt(x) between x=1 and x=4?
This question took quite a bit of thinking until I found a decent way of doing it, although there may be better methods than mine (and I believe the shell method would make this easier).
So I've actually changed
into
(the inverse) because I find it much easier to visualise.
The volume of the original square root function rotated about "y" can be seen as the volume of A (the big green rectangle) rotated about the x-axis, minus the volume of B and C rotated about x-axis (see diagram):
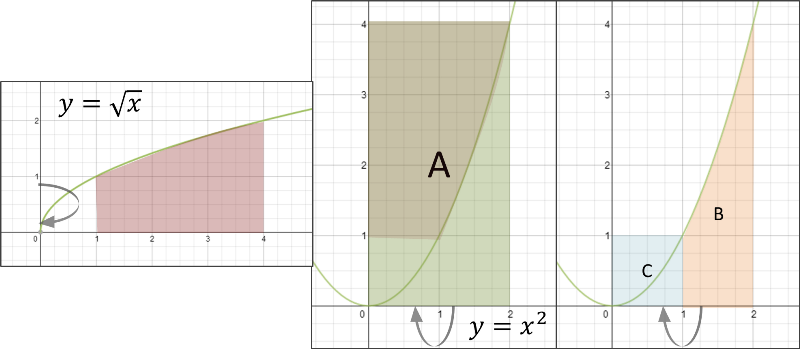
Find volume A and C, they are both cylinders if you rotate them about the x axis:
(2)=32\pi\\\\V_{C} & = & \pi r^{2}h=\pi(1^{2})(1)=\pi\\\end{eqnarray*}\\)
Find volume B, which is the volume when the area under
from x=1 to x=2 is rotated about the x-axis.
^{2}dx=\frac{31\pi}{5}\\)
Hopefully that's correct =p (if not lemme know!)
[edit] fixed slight calculator mistake, thanks kinslayer!
Home
Help
Search
Login
