Bazza's 3/4 Question Thread

[kamil9876]

Yeah certainly, here is one which I think is suitable for VCE level:

I assume that what you're really asking for is "why does Antidifferentiation give me area"

(because more sophisticated definitions of the integral pretty much already give you integral=area just from the definition)


Suppose on

Let denote the area under from to .

We want to show that so let's differentiate A(x):

what we really want to study is:

as

Now is really the area between under between and . So we have the following:



(where and are the point in the interval where is minimum and maximum respectively). Hence dividing by we get that:



Now as we have that and approach and so and approach (technically I'm using the fact that is continous to get the last part)

Hence

[paulsterio]

I think the easier way to think of Kamil's post is to imagine dividing the area up into rectangles, then having the width of the rectangles tend towards 0 and then summing them, it will give the integral

[brightsky]

I think the easier way to think of Kamil's post is to imagine dividing the area up into rectangles, then having the width of the rectangles tend towards 0 and then summing them, it will give the integral

nah that doesn't actually prove that A'(x) = f(x). it simply gives you a way of evaluating A(x).

[paulsterio]

Oh yes, sorry I didn't read it properly, I was thinking that this was the



My bad!

[kamil9876]

Yeah paulsterio's way is why I said at the start that:

I assume that what you're really asking for is "why does Antidifferentiation give me area"

(because more sophisticated definitions of the integral pretty much already give you integral=area just from the definition)

paulsterio had the better definition of integral in mind, but I assumed that sahil26 was interested in the "antiderivative definition"

[paulsterio]

Yep, that makes sense now

[WhoTookMyUsername]

does anyone have a clear definition of a point of inflection?

still not 100% clear on what this concept actually means

for the attached graph, is point C a SPOI?
( i say no, somye says yes, ), but i'm actually not 100% sure what a POI is
i thought it was the place where the gradient is largest, but that's not the case because y=x^3 has a POI at x = 0 D: and dy/dx = 0


it was MC (i'm not sure any answers are right)
the only semi viable ones are

A) B and D represent SPOI
B) A and E are non-stationary POI
C) C is a stationary point of inflection

[Somye]

Note that the original graph is a derivative though Michael

[WhoTookMyUsername]

oh for f**** sake
fml

anyway

what's the best clear definition (practical) of a POI?

[Panicmode]

oh for f**** sake
fml

anyway

what's the best clear definition (practical) of a POI?

A point of inflection occurs if f(x) is continuous at that point and there is a change of concavity at that point.

ie.

f(x) is continuous at point x = a
and f"(x) > 0 for x > a
and f"(x) < 0 for x < a

or

f(x) is continuous at point x = a
and f"(x) > 0 for x < a
and f"(x) < 0 for x > a


Obviously this is conditional upon not running into other turning points in the double derivative but you get the idea.

The basic definition is a point at which a change in concavity occurs

[b^3]

oh for f**** sake
fml

anyway

what's the best clear definition (practical) of a POI?

A point of infection (POI) is where the gradient of the graph changes from increasing () to decreasing() or decreasing() to increasing(), i.e. when the "concavity" changes from +ve to -ve or -ve to +ve. A stationary point of inflection (SPOI) is the just the same except that the gradient is equal to zero at the point where it changes.

E.g. For , the gradient is decreasing () to the left of , but increasing () to the right of , and the gradient is 0 at . So it is a stationary point of inflection.

For the graph is below

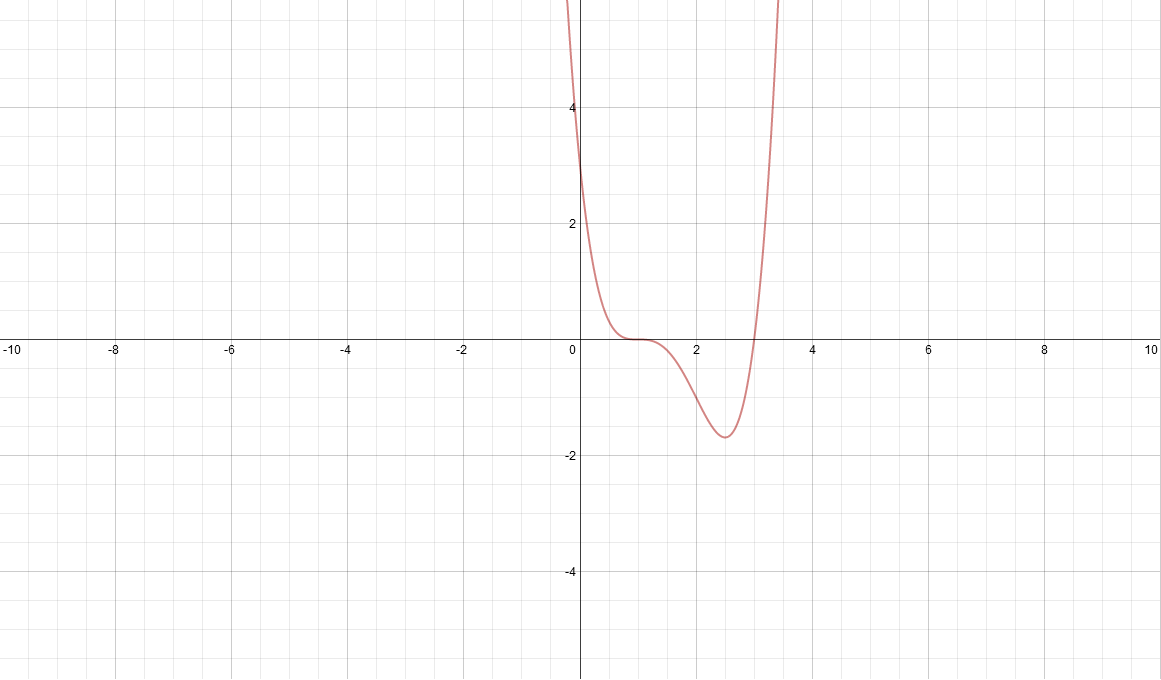
To the left of the gradient is increasing () (it's becoming "less negative") and to the right of the gradient is decreasing (). But at the gradient is 0, that is so we have a SPOI at .

For the graph is below.

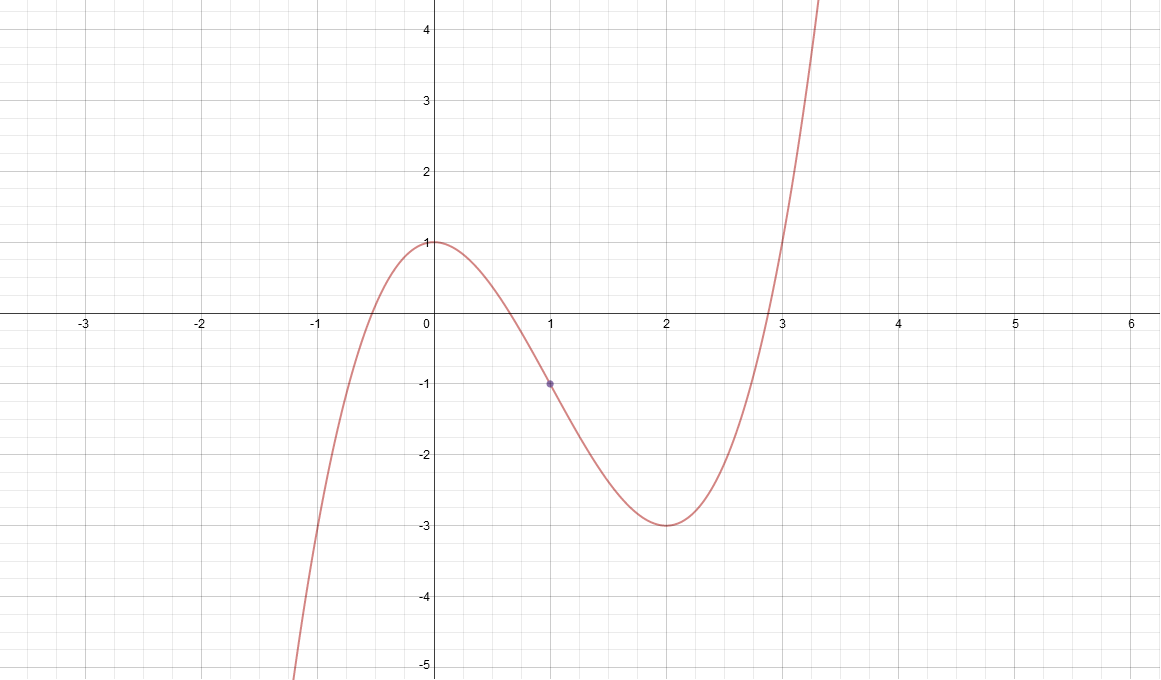
Now looking at , the gradient on the left is decreasing () while the gradient on the right is increasing (). Now this means that we have a point of inflection at but as the gradient isn't 0 at this point, it isn't a SPOI but only a POI.

EDIT: Beaten by Panicmode....but since I typed all this out and generated the graphs I'll post it anyway. Hope the examples help.
EDIT2: Called a POI a stationary point, fixed it up now

[WhoTookMyUsername]

Thanks a lot for those explanations guys

Another q:

Is there any way of rotating something around y, (volume) but where you can't get f(y),

Like can you determine the region rotating around y by considering the region you get when you rotate around x then doing something with this?

[Panicmode]

Thanks a lot for those explanations guys

Another q:

Is there any way of rotating something around y, (volume) but where you can't get f(y),

Like can you determine the region rotating around y by considering the region you get when you rotate around x then doing something with this?

I think I remember reading somewhere that you could rotate around the x-axis using the inverse equation... just need to make sure you get your end points correct.

[WhoTookMyUsername]

Thanks a lot for those explanations guys

Another q:

Is there any way of rotating something around y, (volume) but where you can't get f(y),

Like can you determine the region rotating around y by considering the region you get when you rotate around x then doing something with this?

I think I remember reading somewhere that you could rotate around the x-axis using the inverse equation... just need to make sure you get your end points correct.

Mm... Intresting , thanks for that, anyone know the full process?
I think i know how the inverse applies to area,
If you have f(x) bound to y at say y = 1  and y = 2 then S[inverse f(x)]( terminals 1 and 2) dx is the area bound to y?
( can someone verify thhis
But im not sure how to translate this to volumes

Thanks for everyones help

[Panicmode]

Thanks a lot for those explanations guys

Another q:

Is there any way of rotating something around y, (volume) but where you can't get f(y),

Like can you determine the region rotating around y by considering the region you get when you rotate around x then doing something with this?

I think I remember reading somewhere that you could rotate around the x-axis using the inverse equation... just need to make sure you get your end points correct.

Mm... Intresting , thanks for that, anyone know the full process?
I think i know how the inverse applies to area,
If you have f(x) bound to y at say y = 1  and y = 2 then S[inverse f(x)]( terminals 1 and 2) dx is the area bound to y?
( can someone verify thhis
But im not sure how to translate this to volumes

Thanks for everyones help

Again, I could be completely wrong. This was me studying for my calculus exam at 4 in the morning, 5 hours before the actual exam took place.