Hey everyone! Only a few HSC Physics guides to go, and coincidentally, only a few weeks until Trials! Scary scary stuff, although hopefully these guides are proving at least a little helpful. This one is going to cover the photoelectric effect, something that is a little difficult to understand in parts, so Iíll try to go a little slower than normal. And as always, Iíll be sure to mention potential exam questions and go through them where I think it will help.
As always, remember to register for an account and ask any questions you have below! It takes no time at all, and is an awesome chance to pick the brains of your peers.So, the photoelectric effect. It was first observed by Hertz in 1887. He was investigating radio waves; he induced sparking in one coil, and found that coils near it sparked as well. This was the first observation of radio waves. Hertz calculated the speed of the waves using the wave equation,

. This, of course, was the speed of light we know today,

.
Hertz also noticed that the sparking occurred more readily when the coils were exposed to UV light. He never investigated it, but he had observed the photoelectric effect!
Before we explain it, we need to know a bit about black bodies.
A black body is, theoretically, a perfect absorber and emitter of radiation. There is more complex theory here, but it isnít related to this course. Classical theory falters when attempting to explain black body radiation. Classical theory suggests that, as intensity of radiation increases, frequency should increase also. This means that as the frequencies approach the ultraviolet and gamma end of the EM spectrum, the intensity escalates rapidly, approaching infinity. This makes no sense, and violates the conservation of energy.
Instead, experimental data suggested that radiation was spread over multiple frequencies. This contradiction is known as the
ultraviolet catastrophe .
Planck suggested a solution which, at first, he believed to be just a mathematical trick. He proposed that energy was not released in waves, but in packets, which he called quanta. The energy in each quantum is determined by the frequency of the radiation. Thus, the radiation emitted by a black body is quantised, with the total energy determined based on the number of quanta n, the frequency f, and Planckís Constant h (6.63 ◊ 10−34). Energy per quanta simply removes the n.

A very common HSC question will show you a graph like this, and ask a question on the ultraviolet catastrophe:
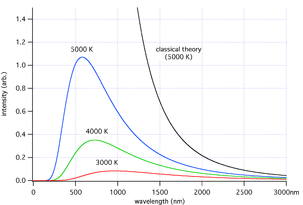
(Image taken from Wikipedia)
Again, simply discuss how classical theory (for extra points, it is actually called Rayleigh Jeans Law) fails to explain intensity at short wavelengths, and how quantum theory proposes a solution.
But how does this tie in to the photoelectric effect? This is where Einstein stepped in. Einstein applied Planckís quantum theories to his model of light, and proposed that light consists of quanta packets, which he called
photons . He also suggested the
All or Nothing Principle , the idea that if a proton collides with something, it either gives up all its energy, or none. Essentially, he maintained that quanta could not be divided.
The particle and wave models of light are linked in a fairly simple way. The particle model of light considers light as small wave packets called photons. An increase in frequency corresponds to an increased amount of energy per photon. The number of photons, rather, is associated with the amplitude of the light waves in wave models. So essentially, higher frequency equals more energy. Larger amplitude means more photons.
Einstein also was able to finally explain the photoelectric effect. The photoelectric effect states that when light of an appropriate frequency is shone onto a metal surface, electrons are emitted from that surface. This occurs due to photons passing their energy to the electrons, allowing them to be ejected from the metal. Ejecting the electron takes energy; this is the
work function φ of the metal. Thus, the kinetic energy K of an emitted electron is:

where E is the energy of the photon.
Every metal has a
threshold frequency , the minimum frequency required for the photons to have enough energy to allow electrons to escape the metal (ie, this is the frequency when the energy per photon is equal to the work function of the metal). Below this frequency, the photoelectric effect does not occur.
Considering the equation K = hf − φ, all of this comes together. It is a linear relationship, where the x intercept is the threshold frequency, the y intercept is the work function, and the gradient is Planckís Constant.

Explaining the photoelectric effect is a common question, as is analysing Einsteinís contributions to the photoelectric effect. Essentially, without Einstein, quantum theory would have remained a mathematical trick with no significance. Einstein brought it into mainstream scientific acceptance.
Let's look at a common, simple math question that I got asked last year:
Example: Calculate the energy of a photon of wavelength 415 nm.
This is just a substitution question utilising Planck's formula and the wave formula:

Remember that photons travel at the speed of light, and make sure you know your more unusual units of measurement. They are a common trick.
Now this topic is all about how ideas are used in everyday stuff. For the photoelectric effect, we need to look at how it is applied in photocells. Let's answer a sample 4 mark question:
Example Two: Explain how the photoelectric effect is applied in a photo cell, and what applications it has.
A photo cell is a device which can detect or measure the amount of incoming light. It works through the photoelectric effect in conjunction with two charged electrodes (a cathode and an anode). The photoelectric effect causes increased electron emission from the cathode, as exposure to light increases. A sensitive circuit measures the photoelectric current generated, and thus, a quantitative measure of light is achieved. Photo cells have applications in light meters (photography), electric eyes, and scientific measuring equipment.

This is about how much detail you would need to guarantee 4 marks; it could absolutely be done in less words. I prefer taking extra words for clearer responses.
And the final little part of this is a little strange. It is also a common HSC question, purely because so few students study it properly. The syllabus asks us to analyse the relationship between science and politics, with reference to Planck and Einstein. Weird huh? Well, here we go...
Much of scientific development is funded by government and politically driven agendas. In the 20th century, this meant the World Wars. Einstein and Planck had different opinions regarding the role of science in politics.
Einstein was a noted pacifist who regularly spoke out against national militarism. He preached separation between science and politics. It is extremely ironic, therefore, that Einstein played a pivotal role in Project Manhattan, the development of the atomic bomb which ended World War 2.
Planck, rather, was a patriot. He accepted that sociopolitical forces guided his science, and indeed, played a large role in the German efforts to develop nuclear arms. We can see therefore, that despite best intentions, science always seems to be rooted in politics and policy.
It is interesting to consider the Ēatomic race.Ē Germany and America conducted identical research towards atomic weapons. However, the political situation at the time meant that Planck and his counterparts were criticised for aiding in war efforts. Einstein was praised for assisting in an ingenious advancement in physics. Again, we see that even with identical work, the response is entirely different.
There are a few way questions can be framed, but this should be more than enough evidence to make a solid discussion point. Questions here are commonly worth 4-6 marks.
And that's it! A few tricky concepts covered here, so be sure to register and ask questions, as many as you like, I am happy to help! Stay tuned for the last few Physics guides over the coming days. Happy study! 
