Going to go over a little bit of theory in the explanation.
So we start off with
=\frac{Ax^{2}+Bx}{x+C})
To find the asymptotes we have to split it up into its fractions, in other words we can long divide as below.
}<br />\\ x+C & |Ax^{2}+Bx<br />\\ (-) & \underline{Ax^{2}+ACx}<br />\\ & \:\:\:\:\:\:(B-AC)x<br />\\ (-) & \:\:\:\:\:\:\underline{(B-AC)x+(BC-AC^{2})}<br />\\ & \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\;\;\;\:\:\:\;\:\:(AC^{2}-BC)<br />\end{alignedat})
So that means that
+\frac{AC^{2}-BC}{x+C})
Now we know there will be a vertical asymptote when the function results in something like

which will be undefined. So that will be when

, so

So we have a vertical asymptote at

. Now we know that

is an asymptote, so that means that here

.
Now for the oblique asymptote, what happens as the fraction part
)
gets smaller and smaller and approaches 0? The function will get closer and closer to
)
, in other words approach it. So now we know that our other asymptote will be
)
, corresponding to

, so that means that

and
=4)
Now solving for B
(1) & =4<br />\\ B & =5<br />\end{alignedat})
So that leaves us with the equation
=\frac{x^{2}+5x}{x+1}=x+4-\frac{4}{x+1})
You don't need all that wordy stuff in the solution, but its just there to explain it (hopefully).
Hope that helps, and hope there are not any mistakes

EDIT: Fixed some of the incomprehendable sentences.
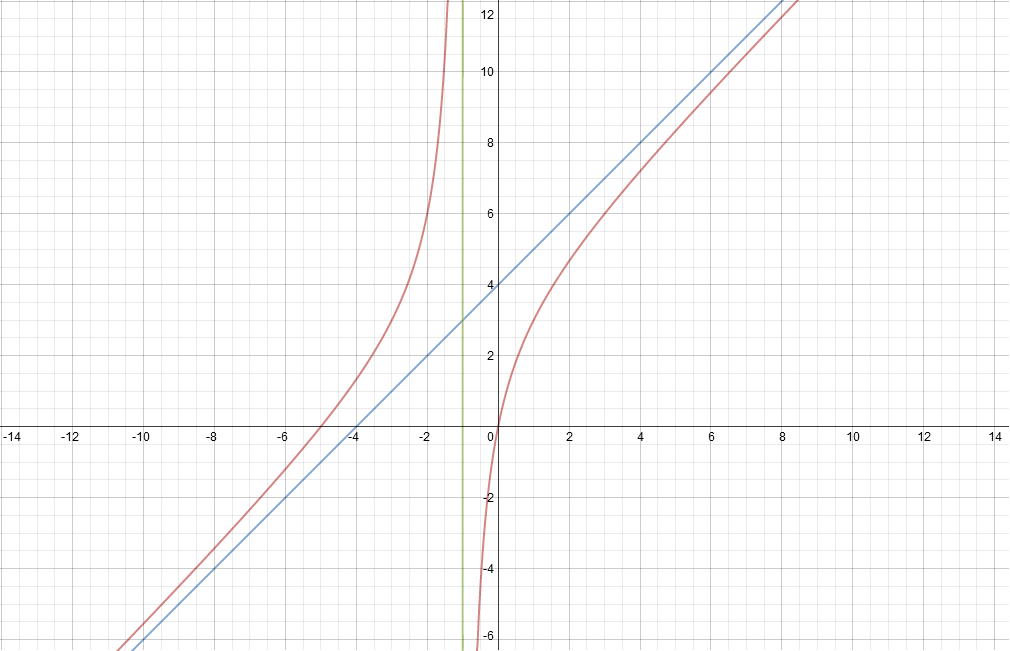
EDIT2: Just thought I'd add the graph so that you can visualise the asymptotic behaviour of the oblique asymptote