I think I may have missed something, as the method that I've used isn't exactly in the course... using trigonometric substitution, but depending on your school you may cover it. Where exactly is the question from?
Anyways, lets start with a circle of radius

shifted

units up from the origin. Here's one I prepared earlier

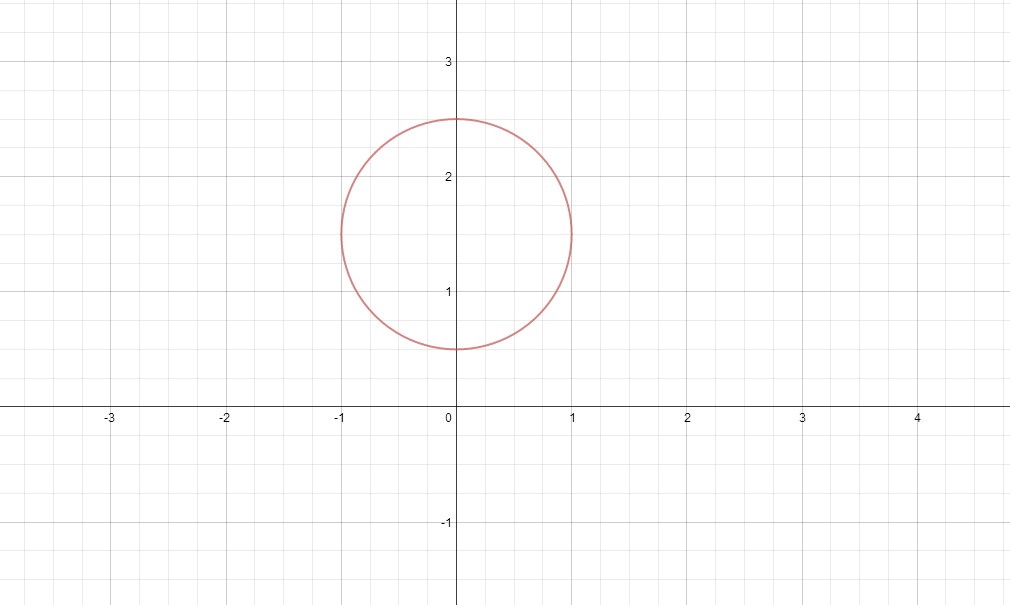
Now that is a circle with equation
^{2}=b^{2})
.
Now for rotation around the

axis we have:

.
So we need

in terms of

.
^{2} & =b^{2}<br />\\ \left(y-a\right)^{2} & =b^{2}-x^{2}<br />\\ y & =a\pm\sqrt{b^{2}-x^{2}}<br />\end{alignedat})
So now we integrate the square of the top curve minus the square of the bottom curve. Since the values of

go from

to

, we have our terminals.
^{2}-\left(a-\sqrt{b^{2}-x^{2}}\right)^{2}dx<br />\\ & =\pi\int_{-b}^{b}a^{2}+2a\sqrt{b^{2}-x^{2}}+b^{2}-x^{2}-\left(a^{2}-2a\sqrt{b^{2}-x^{2}}+b^{2}-x^{2}\right)dx<br />\\ & =\pi\int_{-b}^{b}4a\sqrt{b^{2}-x^{2}}dx<br />\end{alignedat})
Now here comes the bit that isn't on the course.... A trigonometric substitution.
<br />\\ \sqrt{b^{2}-x^{2}} & =\sqrt{b^{2}-b^{2}\sin^{2}\left(\theta\right)}<br />\\ & =\sqrt{b^{2}\left(1-\sin^{2}\left(\theta\right)\right)}<br />\\ & =\sqrt{b^{2}\cos^{2}\left(\theta\right)}<br />\\ & =b\cos\left(\theta\right),\:-\frac{\pi}{2}\leq\theta\leq\frac{\pi}{2}<br />\\ \frac{dx}{d\theta}=b\cos\left(\theta\right)<br />\\ x=b, & \theta=\frac{\pi}{2}<br />\\ x=-b, & \theta=-\frac{\pi}{2}<br />\\ V & =4a\pi\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}b\cos\left(\theta\right)\times b\cos\left(\theta\right)d\theta<br />\\ & =4ab^{2}\pi\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^{2}\left(\theta\right)d\theta<br />\\ & =4ab^{2}\pi\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1+\cos\left(2\theta\right)}{2}d\theta<br />\\ & =2ab^{2}\pi\left[\theta+\frac{1}{2}\sin\left(2\theta\right)\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}<br />\\ & =2ab^{2}\pi\left(\frac{\pi}{2}-0-\left(-\frac{\pi}{2}-0\right)\right)<br />\\ & =2ab^{2}\pi^{2}<br />\end{alignedat}<br /> )
..Although there probably is a way to do it with things that are on the course...
EDIT: Fixed substitution mistake.

