Try applying the transformations and then apply the mod and then last transformation.
i.e.
Start with y=x
2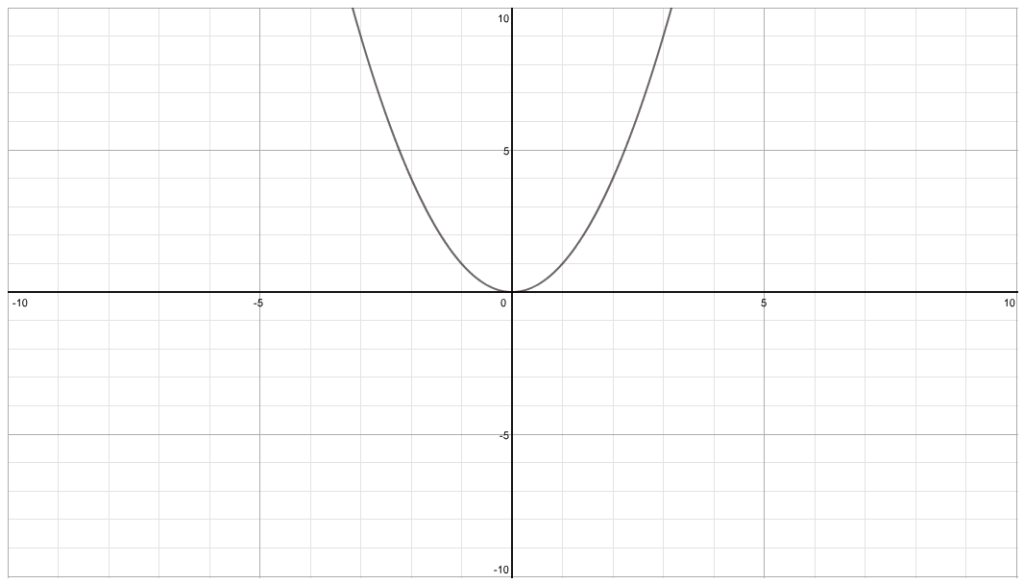
To y=(x+1)
2-1 (translation of 1 unit left and 1 unit down)
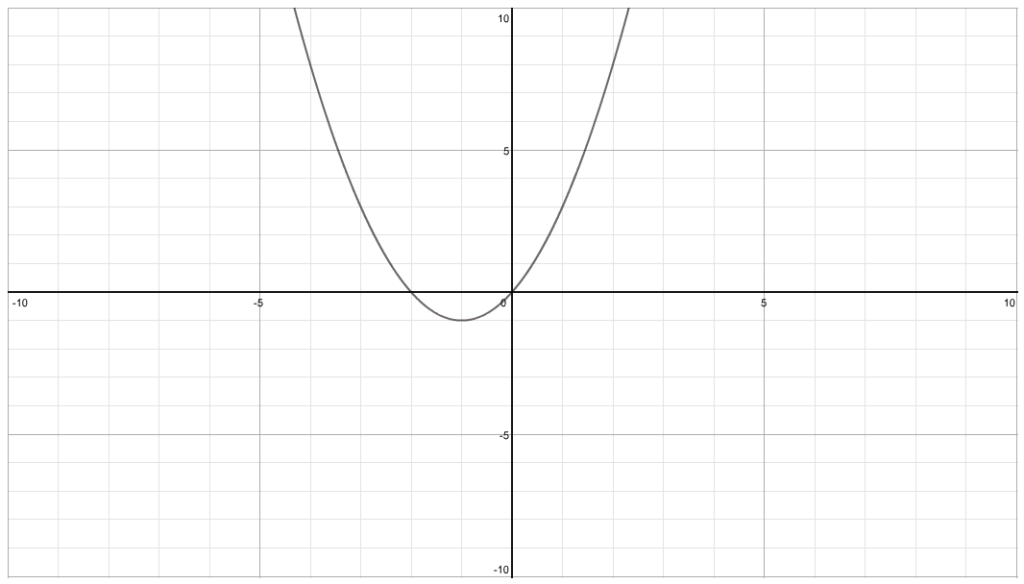
To y=|(x+1)
2-1|. Now the mod will make everything inside that is negative, postivie and everything that is postive to stay positive. That means that anything that is
negative (i.e. below the x-axis) will be
flipped in the x-axis so that it ends up above it and positive.
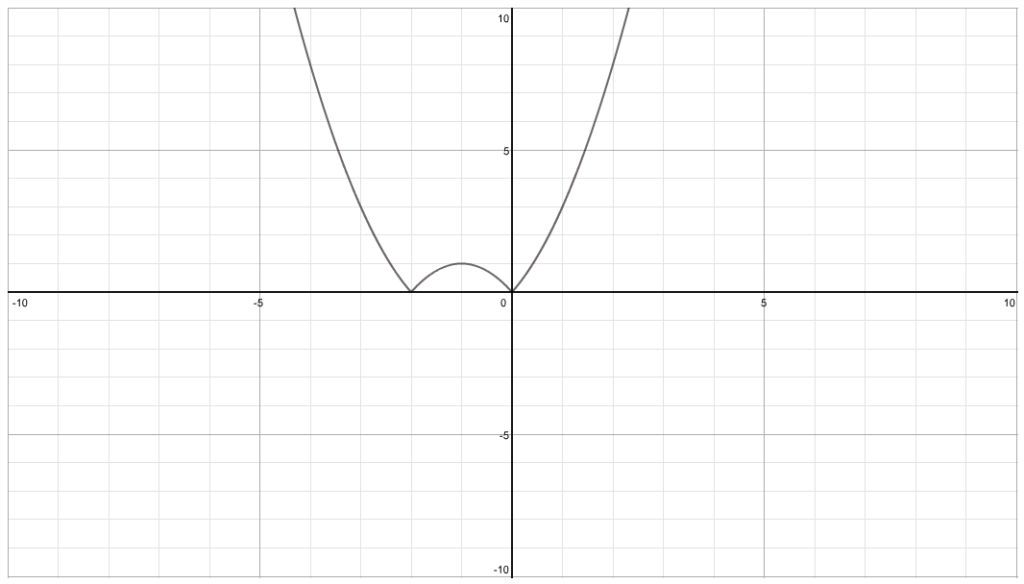
Finally transform to y=|(x+1)
2-1|-2 (a translation of 2 units down).
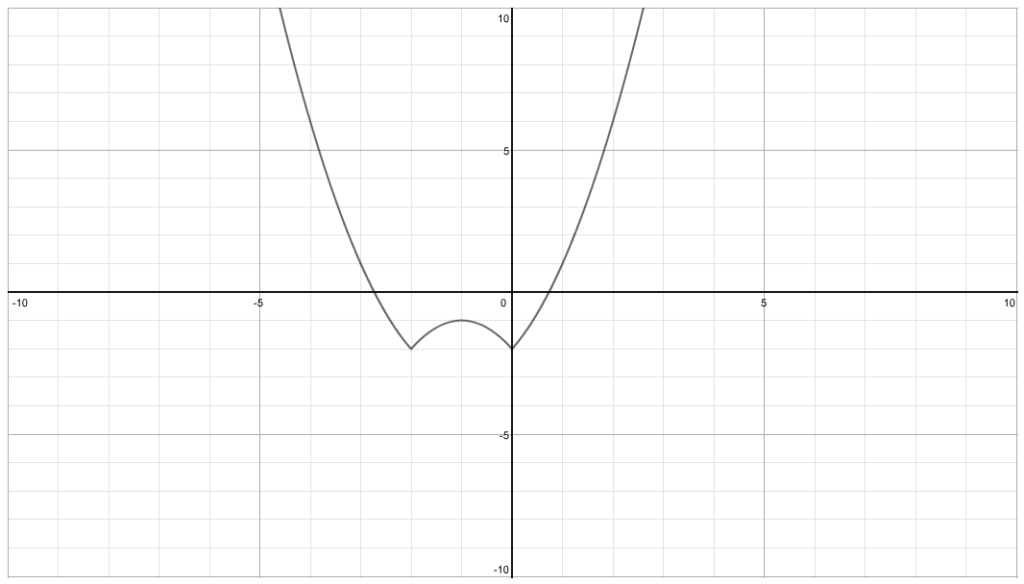
After a while you get used to do all of this in your head, although it is useful to sketch the function before the modulus nd then apply the mod (the flipping the stuff below the a-axis above it).
For x-intercepts/t.ps you can either apply the transformations to the points or for the x-intercepts you can do this.
|(x+1)
2-1|-2=0
|(x+1)
2-1|=2
(x+1)
2-1=2 or -[(x+1)
2-1]=2
(x+1)
2=3 (x+1)
2=-1
x=
no sol
)
,
)
For the turning point, (0,0)-->(-1,-1)-->(-1,1)-->(-1,1-2)=(-1,-1)
y-intercept, x=0
y=|1-1|-2=-2
(0,-2)
Home
Help
Search
Login
