Quick question about calculating flux

[rife168]

Say you have a coil with n turns and the flux through each turn is BA.
If you were asked for the flux through the coil, would it be BA or nBA?

[Howzat]

Wouldn't it be ?

Most of the time, the isn't needed but it depends on the question.

[Aurelian]

Nahhh it's just BA. Flux is just a quantity relating the area of a mathematical surface and a field through that surface; it's just that more often than not - and basically always in VCE - the mathematical surface corresponds to an actual physical surface (e.g. the plane of a loop).

Another thing to consider is Faraday's law of induction at VCE level is given as emf = N(dΦ_b/dt). If you were do use the definition of flux as Φ_b = N(B.A), then you would essentially be counting the number-of-loops factor twice...

[Howzat]

D: That's weird.

I could've sworn I saw this formula in the heinemann book, with the in it.

Regardless, brilliant explanation Aurelian.

[rife168]

Ok that's what I thought, but I just came across this question in Insight 2010:




Originally I answered

But the solution given was just

What do you think is correct?

[Hancock]

Flux is BA. Not nBA. If you have an area of 1m^2, your flux in a 1 Tesla magnetic field is 1. Even if you surround that 1m^2 loop with 100 loops, you still have the same area, and therefore, the same flux through the area.

The solution of your book is right.

[Aurelian]

Ok that's what I thought, but I just came across this question in Insight 2010:

Originally I answered

But the solution given was just

What do you think is correct?

The solution in the book is correct; your method was using the incorrect definition of flux as being nBA. See my previous post for more in depth explanation.

D: That's weird.

I could've sworn I saw this formula in the heinemann book, with the in it.

Regardless, brilliant explanation Aurelian.

The factor of "number of loops" generally comes into play when regarding electromagnetic induction, since Faradays law gives emf = N(dΦb/dt) as mentioned earlier (i.e. the number of loops is relevant).

From what you mentioned, perhaps you might have stumbled across the following generation formula;

emf = nBAωsin(ωt)

This relates the emf generated in a simple generator to the frequency of rotation of the armature windings in the magnetic field. Here you can see that the number of loops is relevant. (It's in Heinemann, but you don't need to know about this formula!)

[paulsterio]

I could tell you that flux is just BA, but that won't mean much to you. This is because flux is a concept which is quite difficult to understand.

In order to actually understand what flux is, you'd need to understand the concept of a vector area. Once this is understood, flux can be defined, simply, as the component of the magnetic field which is passing through a vector surface, S.

Thus, if B is the magnitude of the magnetic field (i.e. magnetic flux density), S is the area of the vector surface, we can consider the magnetic flux through an infinitesimal (very small) area. Let's call that dS, then we have the formula:



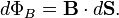
Now, what we can do is change that into a surface integral. Remember how if we take a definite integral of a graph, we split the area under the graph into infinitely small "rectangles" which we then add up? Well a surface integral is a similar concept. It is a definite integral which is taken over a surface. i.e. it is a double integral.



Now doesn't this look familiar? Well it should, because if both B and S are constant, then the flux would simply be, B.S, which is essentially what it is in VCE. Now, the last mathematical thing to note is that, we are multiplying two vectors, B and S. We are looking for the dot product, so essentially:



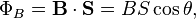
So, for some reason, we use A instead of S in VCE, so swap that around and you're set!