Author Topic: Everything you need to know about Related Rates! (Read 9939 times) Tweet Share

Zealous · « **on:** June 19, 2014, 07:39:39 pm »

Hi!
I’ve seen quite a few questions on Related Rates recently in the forums so I thought I’d write up a guide on how to get started with Related Rates with some tips on how to approach more challenging questions. Personally, I think the textbook didn’t explain Related Rates too well but they are very important as these types of questions come up quite often in VCAA exams. Practice makes perfect with this technique (like a lot of things), so don’t worry if it takes a while at first - hopefully this guide will speed things up.

What is Related Rates all about?
The whole idea of Related Rates in VCE Methods is to express one rate as the product of two or more other rates, essentially creating a connection between them. I’ll illustrate this with a really simple example:

Let’s say there are a few birthday parties for kids happening around Melbourne. Each kid has 20 birthday balloons, and each party has 15 kids attending. So we have two rates:
$20 \ \left(\frac{\text{balloons}}{\text{kids}}\right) \ \ \text{and} \ \ 15 \ \left(\frac{\text{kids}}{\text{party}}\right)$
So how would we find out how many balloons there are per party? We’d multiply the two rates.
$20 \ \left(\frac{\text{balloons}}{\text{kids}}\right) \ \times \ 15 \ \left(\frac{\text{kids}}{\text{party}}\right) = 300 \ \left(\frac{\text{balloons}}{\text{party}}\right)$

By multiplying the balloons/kid by kids/party, we have eliminated the kids (that sounds awkward) and we are left with the balloons/party – our desired rate.

I thought this might be relevant, do not try this at home!

Another simple example is the conversion of units. We know there are 10mm in a cm and 100cm in a metre, so we can express mm/metre as the product of the first two in order to cancel out the cm:
$10 \ \left(\frac{\text{mm}}{\text{cm}}\right)\times100 \ \left(\frac{\text{cm}}{\text{metre}}\right)=1000 \ \left(\frac{\text{mm}}{\text{metre}}\right)$

Here’s the thing which makes it more complicated in Methods. The rates are not always going to be constant. The rates may depend on height, length, time and other different variables.

How do I use the Chain Rule for these questions?
The use of the chain rule is essential when solving these questions. From differential calculus, you should know the chain rule as $\frac{dy}{dx}=\frac{dy}{du} \times \frac{du}{dx}$ where we eliminate the du to leave dy/dx.

For Related Rates, we need to be able to apply the chain rule with different variables so it is important you are fast at setting the chain rule equation up. How do you set it up? Here is a step by step approach:

Let’s take the practical example from the previous section with balloons. Let’s say we want to find out the rate ‘balloons/party’ and we are given the rate ‘kids/party’, how do we know what the unknown/missing rate is?

1: Set up the chain rule using the rate you are trying to find (balloons/party) but break it up into two separate rates:
$\frac{\text{balloons}}{\text{party}}=\frac{\text{balloons}}{?}\times\frac{\text{?}}{\text{party}}$

2: Fill in the rate you are given (kids/party):
$\frac{\text{balloons}}{\text{party}}=\frac{\text{balloons}}{?}\times\frac{\text{kids}}{\text{party}}$

3: Complete the chain rule by introducing a ‘kids’ on the denominator:
$\frac{\text{balloons}}{\text{party}}=\frac{\text{balloons}}{\text{kids}}\times\frac{\text{kids}}{\text{party}}$
So our missing/unknown rate is ‘balloons/kids’.

We can apply this exact same process to other rates. Let’s say we want to find ‘dr/dt’ and we are given ‘dr/dh’

1: Set up the chain rule using the rate you are trying to find (dr/dt) but break it up into two separate rates:
$\frac{dr}{dt}=\frac{dr}{?}\times\frac{?}{dt}$

2: Fill in the rate you are given (dr/dh):
$\frac{dr}{dt}=\frac{dr}{dh}\times\frac{?}{dt}$

3: Complete the chain rule equation by introducing a ‘dh’ onto the numerator:
$\frac{dr}{dt}=\frac{dr}{dh}\times\frac{dh}{dt}$
So our missing/unknown rate is ‘dh/dt’, this would be the rate we would want to find in a Related Rates question.

Try these out: Create a chain rule equation to link the rate we want to ‘Use’ (given rate) and the rate we are trying to ‘Find’.
Example:

$\text{Use} \ \frac{dE}{db} \ \text{to find}: \frac{dE}{dt} \implies \frac{dE}{dt}=\frac{dE}{db}\times\frac{db}{dt}$

Questions:

Spoiler

$1) \ \text{Use} \ \frac{dV}{dr} \ \text{to find}: \frac{dV}{dt}$

$2) \ \text{Use} \ \frac{dt}{dP} \ \text{to find}: \frac{dA}{dP}$

$3) \ \text{Use} \ \frac{dh}{dq} \ \text{to find}: \frac{dh}{ds}$

$4) \ \text{Use} \ \frac{do}{dx} \ \text{to find}: \frac{dB}{dx}$

Answers:

Spoiler

$1) \ \frac{dV}{dt}=\frac{dV}{dr}\times\frac{dr}{dt}$

$2) \ \frac{dA}{dP}=\frac{dA}{dt}\times\frac{dt}{dP}$

$3) \ \frac{dh}{ds}=\frac{dh}{dq}\times\frac{dq}{ds}$

$4) \ \frac{dB}{dx}=\frac{dB}{do}\times\frac{do}{dx}$

Useful tools and tips for solving Related Rates questions:
Now that we have established how to set up the chain rule, here are some useful tools for solving these questions:

Geometry Formulas:
(Note: most of these are available on the formula sheet!)
Area of a Circle: $\pi r^2$ Volume of a Sphere: $\frac{4}{3} \pi r^3$
Volume of a Cone: $\frac{1}{3}\pi r^2 h$ Volume of a Cylinder: $\pi r^2 h$
Volume of a Rectangular Prism: $lwh$ Volume of a Square Based Pyramid: $\frac{1}{3}bh$

Rate Flipping:
$\text{if} \ \frac{dV}{dh}=5\pi \ \implies \ \frac{dh}{dV}=\frac{1}{5 \pi}$
This means we can take the reciprocal (flip) the rate in order to fit it into a chain rule question. So if we can find V in terms of h, differentiate it to get dV/dh, we can then flip it to make dh/dV if our chain rule requires it.

Drawing diagrams:
If you are having issues visualizing certain problems, it can be very useful to draw a diagram so you have a better idea of what you are working with. Do a quick sketch of the situation and label all important features of your diagram.

Similar Triangles:
This is assumed knowledge for Methods so you can be required to use this technique (comes up a lot in cone questions!). If two triangles are similar, the corresponding sides of the triangles are proportional to each other. We can then create an equation to link the two triangles. Make sure you have drawn an appropriate diagram before you set up the fractions:

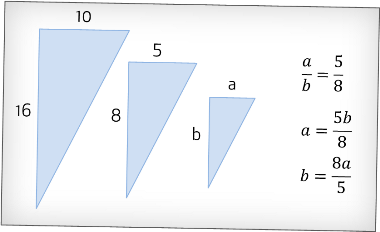How to approach any Related Rates question (with examples!)
Here is a step by step approach to any related rates question – I’ll then run through different examples.

1.   Identify and write down all the key information given. Draw a diagram and define variables if need be. For most Related Rates questions you will be given one rate and told to find another rate with a given condition.

2.   Set up your chain rule equation. Place your resulting rate (the rate you are trying to find) on one side of the equation and the given rate on the other side. Figure out what rate you need to multiply the given rate by in order to complete the chain rule equation.

3.   Using given information in the question, work out the unknown rate. This will most likely require you to use a geometry formula. This can often be the hardest part of a question.

4.   Bring all the information back into the chain rule equation with appropriate substitution. Find your resulting desired rate.

5.   Substitute in any given conditions and present your answer. Don’t forget units!

Example 1:

Quote

The radius of a circular puddle of water is increasing at a rate of 4 cm/s. Find the exact rate at which the area is increasing at the instant the radius is 10 cm.

Worked Solution:

Spoiler

1: Identify and write down all the key information:
$\frac{dr}{dt}=4 \ \ \ \text{Find} \ \frac{dA}{dt} \ \text{when} \ r=10$

Let r=radius of the circle, A=area of the circle and t=time. We have been given dr/dt (the rate in which the radius is changing with respect to time) and the question wants us to find dA/dt (the rate in which the area is changing with respect to time) when r=10.

2: Set up your chain rule equation:
$\frac{dA}{dt}=\frac{dr}{dt}\times\frac{dA}{dr}$

We want our resulting rate to be dA/dt so we can place that on one side of the equation. We are given dr/dt so we should put this on the other side of the equation. From previous sections you should be able to complete the chain rule equation and instantly recognize that if we multiply dr/dt by dA/dr we will get our desired dA/dt.

3: Using given information in the question, work out the unknown rate:
We have just introduced dA/dr into the question, but how do we find out what it is? We need to find out an equation for A in terms of r which we can differentiate. The key information is in the question. The question says “radius of a circular puddle of water”
This means that: $A=\pi r^2 \implies \frac{dA}{dr}=2\pi r$

4: Bring all the information back into the chain rule equation:
Now that we have found what dA/dr is, we can substitute that into the equation we made in Step 3. $\frac{dA}{dt}=\frac{dr}{dt}\times\frac{dA}{dr}=4\times 2\pi r=8\pi r$

This means that our rate of change of the area is dependent on the radius of the circle. When the radius of the circle is smaller, the dA/dt is smaller and when the radius of the circle is larger, the dA/dt is larger.

5: Substitute in any given conditions:
We have found dA/dt but that isn’t our final answer. The question asked for dA/dt when r=10, so we must substitute r=10 into dA/dt.
$\text{When} \ r=10 \ \implies \frac{dA}{dt}=8\pi(10)=80\pi$
Hence when the radius of the puddle is 10cm, the rate of change of the area is $80 \pi \left(\frac{\text{cm}^2}{\text{s}}\right)$ .

Example 2:

Quote

The surface area of a cube is decreasing at a constant rate of 9 cm²/s. Find the rate at which the sides of the cube are decreasing when the sides are 1.5 cm long.

Worked Solution:

Spoiler

1: Identify and write down all the key information:
$\frac{dA}{dt}=-9 \ \ \ \ \text{Find} \ \frac{dL}{dt} \ \text{when} \ L=1.5$ (note the negative because the area is decreasing!)

Let A=surface area of the cube, let S=the side length of the cube and let t=time. We are given dA/dt and we want to find dS/dt (the rate in which the side length is changing with respect to time) when S=1.5.

2: Set up your chain rule equation:
$\frac{dS}{dt}=\frac{dA}{dt}\times\frac{dS}{dA}$

We want our resulting rate to be dS/dr so we can place that on one side of the equation (LHS in this case). We are given dA/dt so we need to multiply this by dS/dA to complete the chain rule equation.

3: Using given information in the question, work out the unknown rate:
We have just introduced dS/dA into the question, but how do we find out what it is? We can first find out what dA/dS is then flip it to get dS/dA. So we need to find out an equation for A in terms of S. The key information is in the question. The question says “the surface area of the cube is decreasing” So it follows that:
$A=6S^2 \implies \frac{dA}{dS}=12S \implies \frac{dS}{dA}=\frac{1}{12S} \ (\text{Flip the rate!})$

4: Bring all the information back into the chain rule equation:
Now that we have found what dS/dA is, we can substitute it into the chain rule equation. So $\frac{dS}{dt}=\frac{dA}{dt}\times\frac{dS}{dA}=-9\times \frac{1}{12S}=-\frac{9}{12S}$

5: Substitute in any given conditions:
The question asks for dS/dt when S=1.5, so sub it in:
$\text{When} \ S=1.5 \ \implies \frac{dS}{dt}=-\frac{9}{12(1.5)}=-\frac{1}{2}$
Hence when the side length of the cube is 1.5cm, the side length is decreasing at a rate of $\frac{1}{2} \left(\frac{\text{cm}}{\text{s}}\right)$

Example 3:

Quote

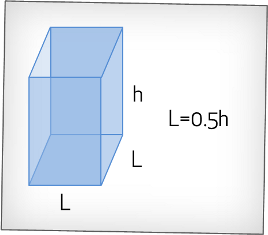
A rectangular block of ice is melting at a rate of 2 cm³/s. The block has a square base and its base length half the height of the block. Find the rate at which the base length is changing when it is 8 cm.

Working Solution:

Spoiler

1: Identify and write down all the key information given.
$\frac{dV}{dt}=-2 \ \ \ \ Let \ L = base \ length \ \ \ Find \ \frac{dL}{dt} \ when \ L=8$

Here is a diagram you might draw up for the example above:

2: Set up your chain rule equation:
$\frac{dL}{dt}=\frac{dV}{dt}\times \frac{dL}{dV}$

3: Our unknown rate is $\frac{dL}{dV}$ How can we find it?
We can find dV/dL first then flip the fraction to make things easier. So first we have to find V in terms of L. Because it has a square base, the volume can be expressed as $V=L^2 \times h$ .

But we cannot differentiate this straight away because there are two variables that change. We want to find dV/dL so we need to get rid of the h. How do we do this? Use the available information to find an equation for h in terms of L - remove the h by introducing an L.

From the question, we know that the base length if half the height of the block. So $L=\frac{1}{2}h \implies h=2L$

We can now sub ‘h’ into the equation so: $V=L^2 \times h \implies V=L^2(2L) = 2L^3$
Now we can differentiate this in terms of L and then flip it to get dL/dV.
$V=2L^3 \implies \frac{dV}{dL}=6L^2 \implies \frac{dL}{dV}=\frac{1}{6L^2} \ (\text{Flip the rate!})$

4: Bring all the information back into the chain rule equation:
$\frac{dL}{dt}=\frac{dV}{dt}\times \frac{dL}{dV}=-2\times\frac{1}{6L^2} =-\frac{1}{3L^2}$

5: Substitute in given conditions:
We want to find dL/dt when L=8, so lets substitute it in:
$\text{When} \ L=8 \ \implies \frac{dL}{dt}=-\frac{1}{3(8)^2}=-\frac{1}{192}$
Hence when the length of the square side of the block is 8cm, the rate in which the length is changing is $-\frac{1}{192}\left(\frac{cm}{s}\right)$

Additional Resources and Examples:
Below I’ve linked a few Related Rates questions from the Methods 3/4 Question Thread and other threads which might be useful to look at:

Cone Question (using Similar Triangles) – Zealous
Cone Question - Stevensmay
Aeroplane Flying and Angles of Elevation – Alwin
Melting Block + Cone of Sand – Zealous
Area underneath a Ladder – Phy124
Cone of Grain – b^3
Streetlights and Shadows – Zealous
Falling Ladder – Stevensmay
Conic Vat pouring into a Swimming Pool – Zealous

There is also a quick vTextbook video on Related Rates where Asher runs through a cylindrical bottle question:
Related Rates – vtextbook.com

Another good video is a video by KhanAcademy (Salman Khan is awesome!) where he runs through a cone question:
Related Rates of Water Pouring into Cone – YouTube

Extra advice for Worded Problems (b^3 and Alwin have some good tips!):
Re: Advice for worded problems?
_______________________________________

So there it is! A guide on how to approach related rates questions. Hopefully this helps you guys out and gives you a better idea of what Related Rates is all about. So what now? Start doing some questions. Your textbook questions + questions available from past VCAA exams will be good practice to apply the techniques explained in this guide. You could even take the questions from the additional examples listed just above if you want (some of them are quite challenging!).

Special thanks to b^3 who helped me make sure everything in this guide is correct and makes sense.

All the best for Methods and the rest of your subjects!

Zealous

vashappenin · « **Reply #1 on:** June 19, 2014, 07:49:09 pm »

Maaaaan I wish I had these posts to refer to when I did methods last year, they seem so useful! Love what you're doing!

speedy · « **Reply #2 on:** June 19, 2014, 07:58:48 pm »

You're amazing man! Keep it up

Rishi97 · « **Reply #3 on:** June 19, 2014, 08:40:09 pm »

Thanks sooo much for taking the time to write this for all in need... i personally struggle with related rates so this has been great

Thanks Zealous

Rod · « **Reply #4 on:** June 20, 2014, 11:08:02 pm »

Awh you beast! Thanks!!

Aye, post us some tips for motion or electric power in physics ......

Reus · « **Reply #5 on:** June 20, 2014, 11:17:39 pm »

Just. What. I. Needed.

Thank. You.

brenden · « **Reply #6 on:** June 21, 2014, 12:24:28 am »

Very admirable.

Phy124 · « **Reply #7 on:** June 21, 2014, 12:51:35 am »

Very nice (Y)

Zealous · « **Reply #8 on:** June 22, 2014, 01:03:13 pm »

Thanks for the comments, I appreciate them!

These guides do take a fair bit of time to create, so it's great that you guys are finding it helpful.

Who knows, if I see a lot of one style of question in the Methods 3/4 Thread I might be back.
(probability is coming up!)

Quote from: Rod on June 20, 2014, 11:08:02 pm

Aye, post us some tips for motion or electric power in physics ......

I'd love to if I was more confident with Physics, but the subject has been messing with my head a bit.

Rod · « **Reply #9 on:** June 22, 2014, 02:25:05 pm »

Quote from: Zealous on June 22, 2014, 01:03:13 pm

Thanks for the comments, I appreciate them!

These guides do take a fair bit of time to create, so it's great that you guys are finding it helpful.

Who knows, if I see a lot of one style of question in the Methods 3/4 Thread I might be back.
(probability is coming up!)
I'd love to if I was more confident with Physics, but the subject has been messing with my head a bit.

nek minit gets a 50 and a premiers award... xD

Tasmania Jones · « **Reply #10 on:** June 23, 2014, 06:08:11 pm »

Nice guide!
Just a minor thing, but the answer to question two should be positive as it asks for the rate of decrease in the question. You are correct in saying that the ROC of the side length is negative, but the question asks for the decrease, which implies a negative ROC

Search the forums now!

We have moved!

Author Topic: Everything you need to know about Related Rates! (Read 9939 times) Tweet Share

Zealous

Everything you need to know about Related Rates!

vashappenin

Re: Everything you need to know about Related Rates!

speedy

Re: Everything you need to know about Related Rates!

Rishi97

Re: Everything you need to know about Related Rates!

Rod

Re: Everything you need to know about Related Rates!

Reus

Re: Everything you need to know about Related Rates!

brenden

Re: Everything you need to know about Related Rates!

Phy124

Re: Everything you need to know about Related Rates!

Zealous

Re: Everything you need to know about Related Rates!

Rod

Re: Everything you need to know about Related Rates!

Tasmania Jones

Re: Everything you need to know about Related Rates!

Recent Posts

User:
Password: