So trigonometry is a major part of the Mathematical Methods 1/2 and 3/4 course, and I know for a fact that many people either struggle with it, or find it difficult to grasp the general gist of the concepts. I believe that the key to overcome this is to master the fundamentals to trig, so that you can manipulate the harder questions. I have decided to comprise a thread dedicated to the introduction of trigonometry, with my explanations of the concepts, including some really helpful links to interactive sites that can assist you in your understandings. I hope you can benefit from this, and if you think a friend can too, feel free to share it!
The Unit Circle:What is it?
The unit circle is a circle plotted on a Cartesian Plane. It has a centre (0, 0) and a radius of one. What does that mean though? It means that (check the image underneath) if you place a point anywhere on the circumference of the circle, the length from the origin to that point will
always be one unit. It's equation is
. There are four areas within the unit circle named quadrants. We name them quadrants 1, 2, 3 and 4 in an anticlockwise direction from the positive x-axis.
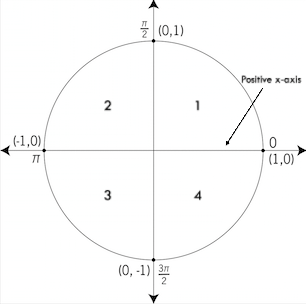
In the image above, we can see that the centre is put on a graph where x-axis and y-axis cross, so we have this neat arrangement. There are four sections named quadrants. We start from the positive x-axis, which is also labelled, and rotate in an anticlockwise direction from there. Angles also play an important role in trigonometry, which essentially define our quadrants.
AnglesWhat are they? Every angle that we will deal with in trigonometry is measured
from the positive x-axis. This feature is very important, and once you can get your head around it, the whole angle process will become easy to you. If we move in an anticlockwise direction from the positive x-axis, our angle will be a positive one. However, if we move in a clockwise direction from the positive x-axis, our angle will be negative. For simple explanations, I will be using degrees instead of radians. It is easier and more effective to understand the degree version, then only you can see how the radian angles work, so:
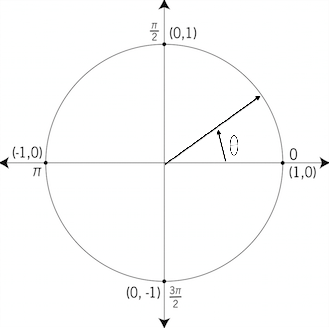
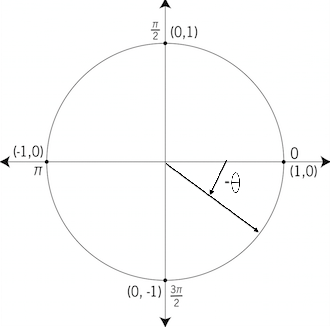
In the first image, because the angle starts from the positive x-axis, and projects in an anticlockwise direction, it is a positive angle. Similarly, the second picture displays a negative angle, as it projects in a clockwise (downwards) direction from the positive x-axis.
This is the way the angles are defined, whenever you see a negative angle, you know it moves clockwise from the positive x-axis, and if you are presented with a positive angle, you should know it moves in an anti clockwise direction.
QuadrantsWhat are they?If we start from the positive x-axis, and move 90 degrees (note: positive angle, hence anti clockwise direction) from the x-axis, we come in contact with the y-axis. This portion is known as quadrant 1 where all the angles contained within are obviously between
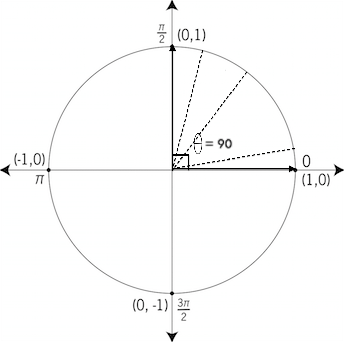
If we continue moving another 90 degrees, we come in contact with the negative x-axis. So, from our original position, (positive x-axis) we have moved a total of 90+90= 180 degrees. Quadrant 2 is defined between 90 and 180 degrees, where all angles in this quadrant are between
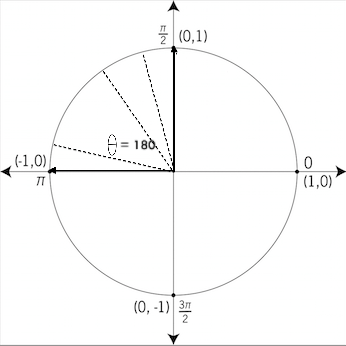
Again, move another 90 degrees, now at 270. Between 180 and 270 is known as quadrant 3, where all angles are between
.
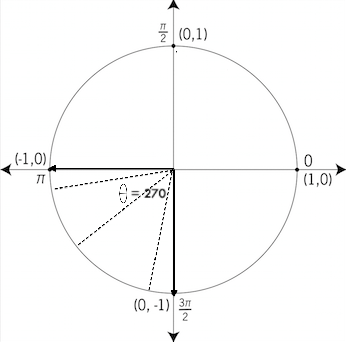
Finally, another 90 degrees and we have made a full anti clockwise rotation of 360 degrees. The portion between 270 to 360 degrees is known as quadrant 4, where all angles are between
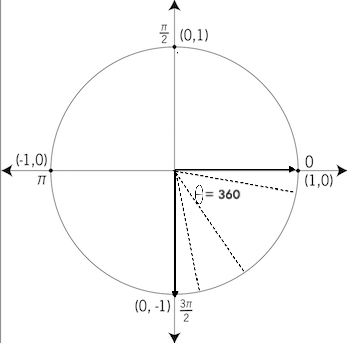Recap:Quadrant
1:
Quadrant
2:
Quadrant
3:
Quadrant
4:
Examples:
SineWhat is it?We define
as the
y-coordinate of point P. This can be thought of as, in simpler terms, the y-coordinate made at the angle
. In the image below, the red arrows represent the y-value or y-coordinate that is made at the angle of theta. This y-value is defined as
. From the properties of the y-axis, we know that the bottom portion of the cartesian plane (the y-axis under the x-axis, the two bottom quadrants: 3 and 4) that the y-axis is negative, hence the sin function is also negative there too. Therefore in the positive y-axis, in quadrants 1 and 2, sin is also positive.
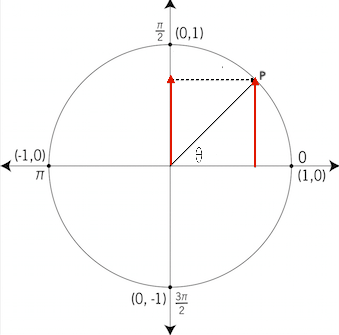CosineWhat is it?We define
as the x-axis of the point P. This too can be thought of as the length of the x-value made at an angle of
. So, from the properties of the x-axis, we know that it is positive on the right side of the Cartesian plane, but negative in the left side of the plane. Therefore cos is also positive in quadrants 1 and 4, but negative in quadrants 2 and 3.
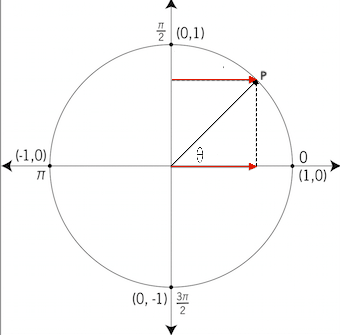TangentWhat is it?The tangent function can be though of as the line x=1, where the ray OP is extended to the point T. Tangent is only positive in quadrants 1 and 3, and negative in quadrants 2 and 4.
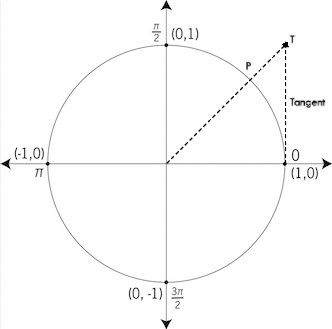Recap: 
:
~ Y-coordinate made at the angle
~ Positive where y-axis is positive (quadrants 1, 2)
~ Negative where y-axis is negative (quadrants 3, 4)
:
~ X-coordinate made at the angle
~ Positive where the x-axis is positive (quadrants 1, 4)
~ Negative where the x-axis is negative (quadrants 2, 3)
:
~ The tangent made through x=1 at the angle
~ Positive in quadrants 1, 3
~ Negative in quadrants 2, 4
Some helpful links:
https://www.mathsisfun.com/geometry/unit-circle.htmlhttps://www.khanacademy.org/math/trigonometry/unit-circle-trig-func/Trig-unit-circle/v/unit-circle-definition-of-trig-functions-1http://www.intmath.com/blog/mathematics/unit-circle-an-introduction-5166http://samples.jbpub.com/9781449606046/06046_CH03_123-178.pdfhttp://online.math.uh.edu/MiddleSchool/Modules/Module_4_Geometry_Spatial/Content/UnitCircleTrigonometry-TEXT.pdfhttps://www.youtube.com/watch?v=cIVpemcoAlYhttps://www.youtube.com/watch?v=YK7KoU6ELWghttps://www.youtube.com/watch?v=j5SoWzBSUmYI hope you understood what was said above, if you have any problems, suggestions or questions please do not hesitate to PM me, or leave a comment on this thread! Thank you!
Part 2:
How NOT to Memorise Exact Values! - Trigonometry
Home
Help
Search
Login
