sin(x) + cos(x) = 1

[gta007]

Okay guys/gals:

Was attempting this question and my answer answer turned out the same with the book, however some solutions I got from doing the question weren't actually part of the solution to the question. I'm not sure if you understand me, but here's the maths"

sinx + cosx = 1
Square both sides:
sin^2x + 2sinxcosx + cos^2x = 1
1 + 2sinxcosx = 1
2sinxcosx = 0
sinxcosx = 0

sinx = 0
thus x = 0. pi, 2pi

cosx = 0
thus x = pi/2, 3pi/2

So the solutions are 0, pi/2, pi, 3pi/2, 2pi.........
But after checking it was seen that 3pi/2 and pi weren't solutions as when substituted into sinx + cosx it would give -1.

Thus I came to the final solution of 0, pi/2, 2pi. I posted this here to see if there was another way to get to the final solution without having to check if they were solutions to the question.

Any help is much appreciated. 

[midas_touch]

When you square both sides in the first step, you are solving for both +/-1, since -1 squared is also 1. Even if you take the square root of both sides at the end, it isnt of much help. However a way around this is using the unit circle to eliminate the pi and 3pi/2 solutions, since these solutions respectively give sinx = 0, cosx = -1 and sinx = -1, cosx = 0.

[dcc]

For the solution to be one, then obviously both sin(x) and cos(x) must be positive OR one of them zero. (i.e. sin(x) = 1 when cos(x) = 0 and cos(x) = 1 when sin(x) = 0)

Whenever sin(x) is 0 and cos(x) is 1, we will have a solution, so finding these solutions, we get:





Now the other solutions will come when cos(x) is 0 and sin(x) is 1, so finding those solutions:





These two conditions are the only way that sin(x) + cos(x) = 1 can be true

Just for your interest, try graphing all the graphs of the solutions when you square both sides, you'll notice that there are twice as many solutions as you want!

[dcc]

Another interesting thing, if you consider the unit circle, it has a radius of 1, and the x-coordinate of any point on that circle is cos(x) and the y-coordinate is the sin(x) of that point.

PICTURE:


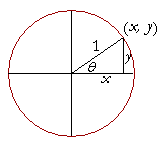
in this picture, and

now we are trying to find when , let us call a point on the unit-circle.

Now, for sin(x) + cos(x) to equal 1, then the point is because the x-coordinate of P represents and the y-coordinate represents

Vector OP is the line from the origin to our point P and OP has length 1 (as this is the unit circle), so:



now, dotting this vector with itself, we get:



And since we know , then:



Expanding & simplifying & canceling, we get:



therefore:

so will be true when our point is:

(which represent when cos(x) = 0 and sin(x) = 1 AND cos(x) = 1 and sin(x) = 0, respectively)

so these simplify to the two above equations which i gave

[Ahmad]

Multiply both sides by



Spot the sine addition formula pattern.

[gta007]

Thanks for the help guys, gave me an insight to the different ways to solve the problem.