The modulus will take any negative number, and make it into a positive number of the same magnitude, and leave everything else as in. This means that when we apply the modulus to

, we are effectively taking the region of the graph for which
<0)
, that is it is below the

axis and flipping in the

axis, (I should note this only applies when we apply the modulus to the
outside of a function, i.e.
|)
, the case where it is applied to the inside of a function, i.e.
)
is different). Then for the graph above we'll shift that resulting graph upwards by one unit.
For the

and

intercepts, we have
<br />\\ y=0<br />\\ |x-3|+1 & =0<br />\\ |x-3| & =-1<br />\end{alignedat})
Now if

, (so

) then the modulus won't do anything to out line. If

(so

), then our line is flipped, and we need to include a negative, as we effectively have
)
 & =-1<br />\\ x-3 & =1<br />\\ x & =4,\:\text{But }x< 3<br />\end{alignedat})
So as our solutions don't satisfy each particular part we don't have an

intercepts, but we do have a

intercept at
)
.
Now the only part we are missing is the sharp point, as we know that the sharp point of
=|x|)
is at
)
, then applying the transformations we get the sharp point at
)
(you could also look at this by solving what is inside the modulus and equating that to zero, as this is where our original curve is 'flipped').
So applying the transformations one by one we have:

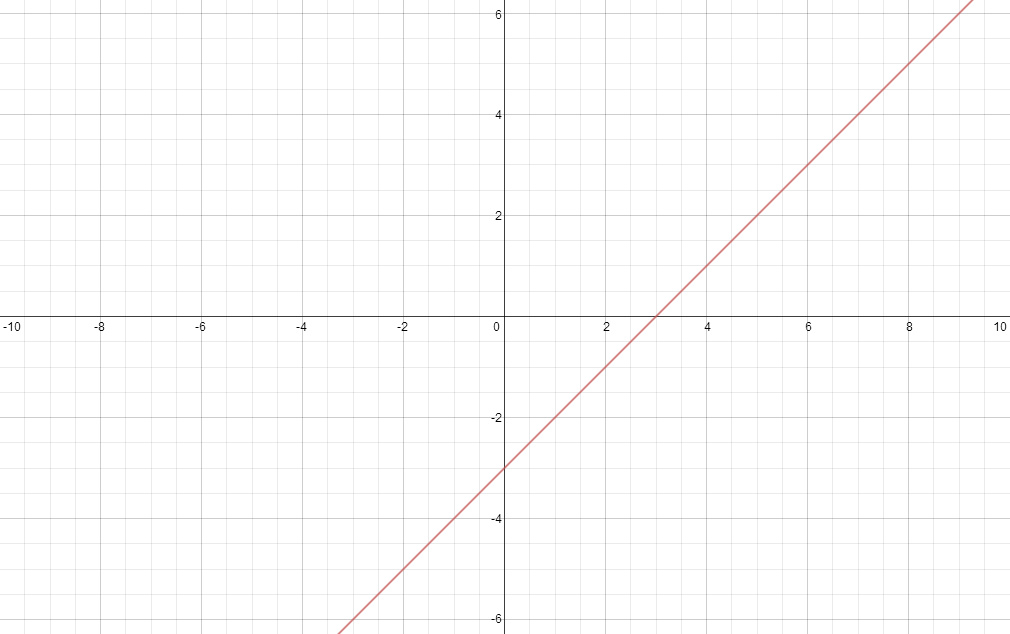

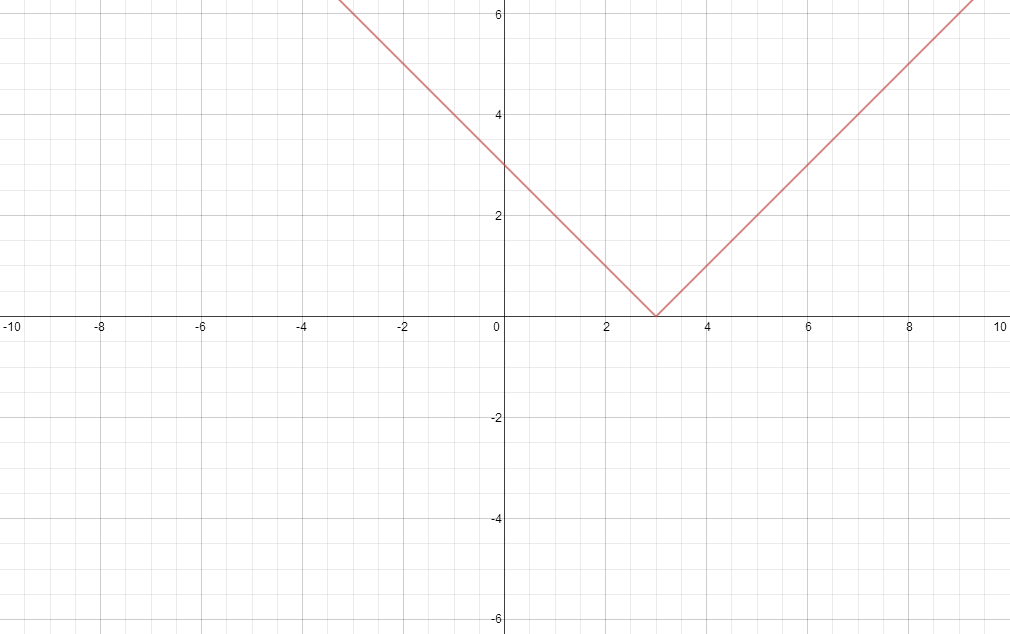

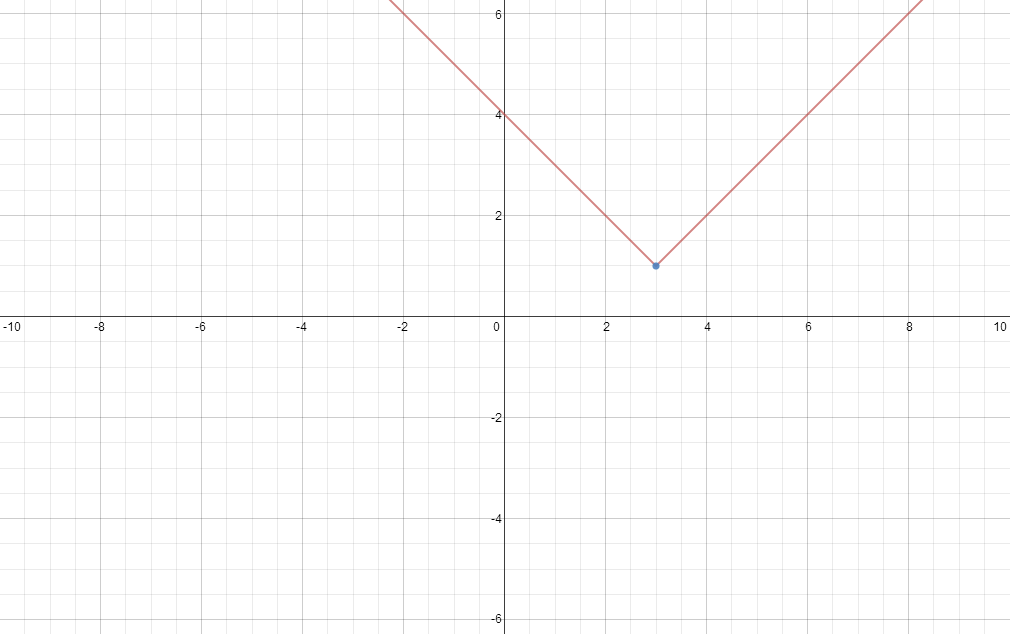
With the second, follow the same method, just remember to have that negative in there.
Hope that helps! I feel I may have explained it in a round about way merging two methods.... but hope you take something from it anyways.
EDIT: Beaten, shouldn't have spent time in plotting the graphs


