You're on the right track with your reasoning. Think of it this way, with
))
you're putting an input

into the

, to give an output

, which is then taken as the input to

. We can only input things into

which give an output of

, that is whatever we put into

should be within the maximal domain of

, otherwise it'll come out as undefined (for example if we had
=\frac{1}{x-1})
and we tried to put an output of

,
=1)
into

, it wouldn't work as

would come out as undefined). Now what are we putting into

? The output of

, so this means that the range of

has to 'fit into
the domain of

, so that anything we put into

will give an acceptable output that can then be put into

.
Now as to why the domain of
))
is equal to the domain of
)
. What you're originally doing is inputting into

, this initial input will be your domain of the whole function, but remember it has to be accepted by

and also has to give an output that is accepted by

. If we know that we've restricted the function (if necessary) so that it will be accepted by

, then these values we are putting into the composite function are just the domain of

.
Since we want
))
, we need to restrict

such that the range of

is equal to or a subset of the domain of

. Since we are restricting

, we can't change

so we can first look at the domain of

, which is

. So now we want to restrict

so that it's range is
\leq 3)
. If we do a quick sketch we get the graph below.
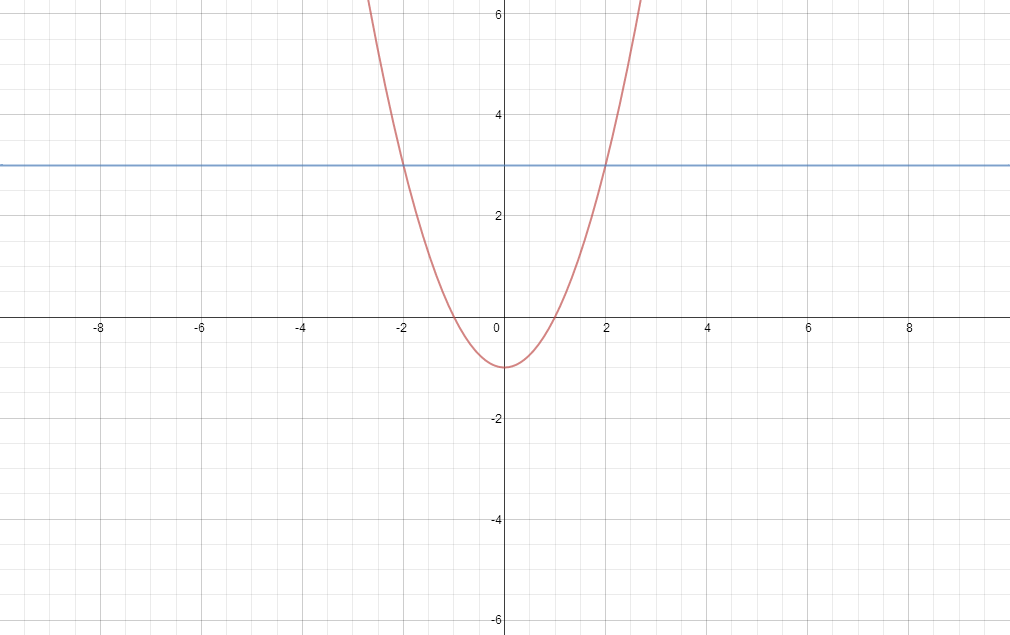
Now if we solve for when we have
=3)
we have,

Now as we can see from the graph,

will be less than or equal to

for

. So that becomes our restricted domain of

.
=x^{2}-1\end{alignedat})
Now now matter what you put into

given the new domain, you'll always get an output that can then be 'accepted' into

.
Hope that helps


